

| Creating and Manipulating Models |   |
Model Dynamics
The Control System Toolbox offers commands to determine the system poles, zeros, DC gain, norms, etc. You can apply these commands to single LTI models or LTI arrays. The following table gives an overview of these commands.
| Model Dynamics | |
|
Covariance of response to white noise. |
|
Natural frequency and damping of system poles. |
|
Low-frequency (DC) gain. |
|
Sort discrete-time poles by magnitude. |
|
Sort continuous-time poles by real part. |
|
Norms of LTI systems (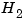 and and 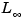 ). ). |
|
System poles. |
|
Pole/zero map. |
|
System transmission zeros. |
With the exception of 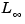
norm, these commands are not supported for FRD models.
Here is an example of model analysis using some of these commands.
h = tf([4 8.4 30.8 60],[1 4.12 17.4 30.8 60]) Transfer function: 4 s^3 + 8.4 s^2 + 30.8 s + 60 --------------------------------------- s^4 + 4.12 s^3 + 17.4 s^2 + 30.8 s + 60 pole(h) ans = -1.7971 + 2.2137i -1.7971 - 2.2137i -0.2629 + 2.7039i -0.2629 - 2.7039i zero(h) ans = -0.0500 + 2.7382i -0.0500 - 2.7382i -2.0000 dcgain(h) ans = 1 [ninf,fpeak] = norm(h,inf)% peak gain of freq. response ninf = 1.3402 % peak gain fpeak = 1.8537 % frequency where gain peaks
These functions also operate on LTI arrays and return arrays. For example, the poles of a three dimensional LTI array sysarray are obtained as follows.
sysarray = tf(rss(2,1,1,3)) Model sysarray(:,:,1,1) ======================= Transfer function: -0.6201 s - 1.905 --------------------- s^2 + 5.672 s + 7.405 Model sysarray(:,:,2,1) ======================= Transfer function: 0.4282 s^2 + 0.3706 s + 0.04264 ------------------------------- s^2 + 1.056 s + 0.1719 Model sysarray(:,:,3,1) ======================= Transfer function: 0.621 s + 0.7567 --------------------- s^2 + 2.942 s + 2.113 3x1 array of continuous-time transfer functions. pole(sysarray) ans(:,:,1) = -3.6337 -2.0379 ans(:,:,2) = -0.8549 -0.2011 ans(:,:,3) = -1.6968 -1.2452
 | Model Analysis Tools | State-Space Realizations |  |