Function Reference

covar

Output and state covariance of a system driven by white noise

Syntax

• [P,Q] = covar(sys,W)
  

Description

covar calculates the stationary covariance of the output 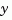of an LTI model sys driven by Gaussian white noise inputs 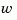. This function handles both continuous- and discrete-time cases.

P = covar(sys,W) returns the steady-state output response covariance

given the noise intensity

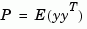
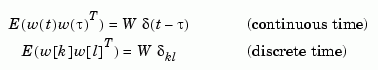
[P,Q] = covar(sys,W) also returns the steady-state state covariance

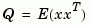
when sys is a state-space model (otherwise Q is set to []).

When applied to an N-dimensional LTI array sys, covar returns multi-dimensional arrays P, Q such that

P(:,:,i1,...iN) and Q(:,:,i1,...iN) are the covariance matrices for the model sys(:,:,i1,...iN).

Example

Compute the output response covariance of the discrete SISO system

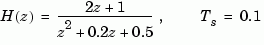
due to Gaussian white noise of intensity W = 5. Type

• sys = tf([2 1],[1 0.2 0.5],0.1);
  p = covar(sys,5)
  

and MATLAB returns

• p =
      30.3167
  

You can compare this output of covar to simulation results.

• randn('seed',0)
  w = sqrt(5)*randn(1,1000);  % 1000 samples
  
  % Simulate response to w with LSIM:
  y = lsim(sys,w);
  
  % Compute covariance of y values
  psim = sum(y .* y)/length(w);
  

This yields

• psim = 
      32.6269
  

The two covariance values p and psim do not agree perfectly due to the finite simulation horizon.

Algorithm

Transfer functions and zero-pole-gain models are first converted to state space with ss.

For continuous-time state-space models

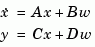
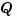is obtained by solving the Lyapunov equation

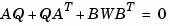
The output response covariance 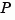is finite only when 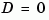and then .

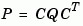In discrete time, the state covariance solves the discrete Lyapunov equation

and is given by

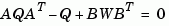
Note that 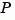is well defined for nonzero 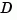in the discrete case.

Limitations

The state and output covariances are defined for stable systems only. For continuous systems, the output response covariance 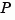is finite only when the 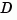matrix is zero (strictly proper system).

See Also
dlyap       Solver for discrete-time Lyapunov equations

lyap        Solver for continuous-time Lyapunov equations

References

[1] Bryson, A.E. and Y.C. Ho, Applied Optimal Control, Hemisphere Publishing, 1975, pp. 458-459.

connect

ctrb