

| Mathematics |   |
The function bvp4c solves a class of singular BVPs of the form
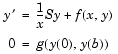
|
(14-3) |
It can also accommodate unknown parameters for problems of the form
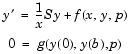
Singular problems must be posed on an interval 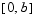 with
with 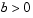 . Use
. Use bvpset to pass the constant matrix 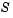 to
to bvp4c as the value of the 'SingularTerm' integration property. Boundary conditions at 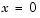 must be consistent with the necessary condition for a smooth solution,
must be consistent with the necessary condition for a smooth solution, 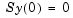 . An initial guess should also satisfy this necessary condition.
. An initial guess should also satisfy this necessary condition.
When you solve a singular BVP using
bvp4c requires that your function odefun(x,y) return only the value of the 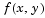 term in Equation 14-3.
term in Equation 14-3.
Example: Solving a BVP that Has a Singular Term
Emden's equation arises in modeling a spherical body of gas. The PDE of the model is reduced by symmetry to the ODE
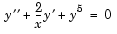
on an interval 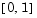 . The coefficient
. The coefficient 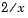 is singular at
is singular at 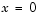 , but symmetry implies the boundary condition
, but symmetry implies the boundary condition 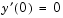 . With this boundary condition, the term
. With this boundary condition, the term
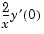
is well-defined as 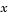 approaches 0. For the boundary condition
approaches 0. For the boundary condition 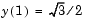 , this BVP has the analytical solution
, this BVP has the analytical solution
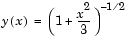
Note
The demo emdenbvp contains the complete code for this example. The demo uses subfunctions to place all required functions in a single M-file. To run this example type emdenbvp at the command line. See BVP Solver Basic Syntax and Solving BVP Problems for more information.
|
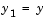 and
and 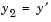 , write the differential equation as a system of two first-order equations
, write the differential equation as a system of two first-order equations
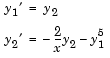
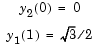
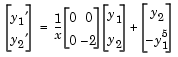
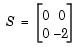
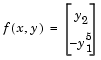
bvp4c can use.
function dydx = emdenode(x,y) dydx = [ y(2) -y(1)^5 ]; function res = emdenbc(ya,yb) res = [ ya(2) yb(1) - sqrt(3)/2 ];
'SingularTerm' integration property.
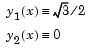
bvpinit to form the guess structure
bvp4c syntax to solve the problem.
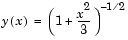
bvp4c.
 | Using Continuation to Make a Good Initial Guess | Changing BVP Integration Properties |  |