Mathematics

Using Continuation to Make a Good Initial Guess

To solve a boundary value problem, you need to provide an initial guess for the solution. The quality of your initial guess can be critical to the solver performance, and to being able to solve the problem at all. However, coming up with a sufficiently good guess can be the most challenging part of solving a boundary value problem. Certainly, you should apply the knowledge of the problem's physical origin. Often a problem can be solved as a sequence of relatively simpler problems, i.e., a continuation. This section provides examples that illustrate how to use continuation to:

• Solve a difficult BVP.
• Verify a solution's consistent behavior.

Example: Using Continuation to Solve a Difficult BVP

This example solves the differential equation

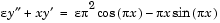
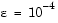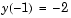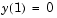for , on the interval [-1 1], with boundary conditions and . For 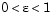, the solution has a transition layer at 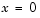. Because of this rapid change in the solution for small values of 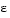, the problem becomes difficult to solve numerically.

The example solves the problem as a sequence of relatively simpler problems, i.e., a continuation. The solution of one problem is used as the initial guess for solving the next problem.

Note    The demo shockbvp contains the complete code for this example. The demo uses subfunctions to place all required functions in a single M-file. To run this example type shockbvp at the command line. See BVP Solver Basic Syntax and Solving BVP Problems for more information.

Note    This problem appears in [1] to illustrate the mesh selection capability of a well established BVP code COLSYS.

1. Code the ODE and boundary condition functions. Code the differential equation and the boundary conditions as functions that bvp4c can use. Because there is an additional known parameter 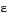, the functions must be of the form

• dydx = odefun(x,y,p1)
  res = bcfun(ya,yb,p1)
  

1. The code below represents the differential equation and the boundary conditions in the functions shockODE and shockBC. Note that shockODE is vectorized to improve solver performance. The additional parameter 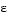is represented by e.

   • function dydx = shockODE(x,y,e)
     pix = pi*x;
     dydx = [  y(2,:)
              -x/e.*y(2,:) - pi^2*cos(pix) - pix/e.*sin(pix) ];
     
     function res = shockBC(ya,yb,e)
     res = [ ya(1)+2 
             yb(1)   ];
     

   The example passes e as an additional input argument to bvp4c.

   •   sol = bvp4c(@shockODE,@shockBC,sol,options,e);
     

   bvp4c then passes this argument to the functions shockODE and shockBC when it evaluates them. See Additional BVP Solver Arguments for more information.

2. Provide analytical partial derivatives. For this problem, the solver benefits from using analytical partial derivatives. The code below represents the derivatives in functions shockJac and shockBCJac.

• function jac = shockJac(x,y,e)
  jac = [ 0   1
          0 -x/e ];
  
  function [dBCdya,dBCdyb] = shockBCJac(ya,yb,e)
  dBCdya = [ 1 0
             0 0 ];
  dBCdyb = [ 0 0
             1 0 ];
  

1. shockJac and shockBCJac must accept the additional argument e, because bvp4c passes the additional argument to all the functions the user supplies.

   Tell bvp4c to use these functions to evaluate the partial derivatives by setting the options FJacobian and BCJacobian. Also set 'Vectorized' to 'on' to indicate that the differential equation function shockODE is vectorized.

   • options = bvpset('FJacobian',@shockJac,...
                      'BCJacobian',@shockBCJac,...
                      'Vectorized','on');
     

3. Create an initial guess. You must provide bvp4c with a guess structure that contains an initial mesh and a guess for values of the solution at the mesh points. A constant guess of 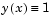and 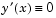, and a mesh of five equally spaced points on [-1 1] suffice to solve the problem for 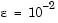. Use bvpinit to form the guess structure.

• sol = bvpinit([-1 -0.5 0 0.5 1],[1 0]);
  

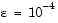4. Use continuation to solve the problem. To obtain the solution for the parameter , the example uses continuation by solving a sequence of problems for 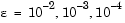. The solver bvp4c does not perform continuation automatically, but the code's user interface has been designed to make continuation easy. The code uses the output sol that bvp4c produces for one value of e as the guess in the next iteration.

• e = 0.1; 
  for i=2:4 
      e = e/10; 
      sol = bvp4c(@shockODE,@shockBC,sol,options,e); 
  end
  

5. View the results. Complete the example by displaying the final solution

• plot(sol.x,sol.y(1,:))
  axis([-1 1 -2.2 2.2])
  title(['There is a shock at x = 0 when \epsilon = '... 
        sprintf('%.e',e) '.']) 
  xlabel('x')
  ylabel('solution y')
  
  
  

Example: Using Continuation to Verify a Solution's Consistent Behavior

Falkner-Skan BVPs arise from similarity solutions of viscous, incompressible, laminar flow over a flat plate. An example is

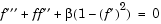
for 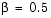on the interval 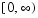with boundary conditions 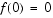, , 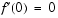and .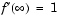

The BVP cannot be solved on an infinite interval, and it would be impractical to solve it for even a very large finite interval. So, the example tries to solve a sequence of problems posed on increasingly larger intervals to verify the solution's consistent behavior as the boundary approaches .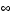

The example imposes the infinite boundary condition at a finite point called infinity. The example then uses continuation in this end point to get convergence for increasingly larger values of infinity. It uses bvpinit to extrapolate the solution sol for one value of infinity as an initial guess for the new value of infinity. The plot of each successive solution is superimposed over those of previous solutions so they can easily be compared for consistency.

Note    The demo fsbvp contains the complete code for this example. The demo uses subfunctions to place all required functions in a single M-file. To run this example type fsbvp at the command line. See BVP Solver Basic Syntax and Solving BVP Problems for more information.

1. Code the ODE and boundary condition functions. Code the differential equation and the boundary conditions as functions that bvp4c can use.

• function dfdeta = fsode(eta,f)
  beta = 0.5;
  dfdeta = [ f(2)
             f(3)
            -f(1)*f(3) - beta*(1 - f(2)^2) ];
  
  function res = fsbc(f0,finf)
  res = [f0(1)
         f0(2)
         finf(2) - 1];
  

2. Create an initial guess. You must provide bvp4c with a guess structure that contains an initial mesh and a guess for values of the solution at the mesh points. A crude mesh of five points and a constant guess that satisfies the boundary conditions are good enough to get convergence when infinity = 3.

• infinity = 3;
  maxinfinity = 6;
  
  solinit = bvpinit(linspace(0,infinity,5),[0 0 1]);
  

3. Solve on the initial interval. The example obtains the solution for infinity = 3. It then prints the computed value of 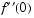for comparison with the value reported by Cebeci and Keller [2].

• sol = bvp4c(@fsode,@fsbc,solinit);
  eta = sol.x;
  f = sol.y;
  
  fprintf('\n');
  fprintf('Cebeci & Keller report that f''''(0) = 0.92768.\n')
  fprintf('Value computed using infinity = %g is '...
          '%7.5f.\n',Bnew,f(3,1))
  

1. The example prints

   • Cebeci & Keller report that f''(0) = 0.92768.
     Value computed using infinity = 3 is 0.92915.
     

4. Setup the figure and plot the initial solution.

• figure
  plot(eta,f(2,:),eta(end),f(2,end),'o');
  axis([0 maxinfinity 0 1.4]);
  title('Falkner-Skan equation, positive wall shear, \beta = 0.5.')
  xlabel('\eta')
  ylabel('df/d\eta')
  hold on
  drawnow 
  shg 
  
  
  

5. Use continuation to solve the problem and plot susbsequent solutions. The example then solves the problem for infinity = 4, 5, 6. It uses bvpinit to extrapolate the solution sol for one value of infinity as an initial guess for the next value of infinity. For each iteration, the example prints the computed value of 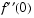and superimposes a plot of the solution in the existing figure.

• for Bnew = infinity+1:maxinfinity
    
    solinit = bvpinit(sol,[0 Bnew]); % Extend solution to Bnew.
    sol = bvp4c(@fsode,@fsbc,solinit);
    eta = sol.x;
    f = sol.y;
    
    fprintf('Value computed using infinity = %g is '...
            '%7.5f.\n',Bnew,f(3,1))
    plot(eta,f(2,:),eta(end),f(2,end),'o');
    drawnow
    
  end
  hold off
  

1. The example prints

   • Value computed using infinity = 4 is 0.92774.
     Value computed using infinity = 5 is 0.92770.
     Value computed using infinity = 6 is 0.92770.
     

   Note that the values approach 0.92768 as reported by Cebeci and Keller. The superimposed plots confirm the consistency of the solution's behavior.

   

Solving BVP Problems

Solving Singular BVPs