

| Mathematics |   |
Solving BVP Problems
bvp4c
Example: Mathieu's Equation
This example determines the fourth eigenvalue of Mathieu's Equation. It illustrates how to write second-order differential equations as a system of two first-order ODEs and how to use bvp4c to determine an unknown parameter 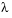 .
.
The task is to compute the fourth (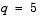 ) eigenvalue
) eigenvalue 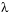 of Mathieu's equation
of Mathieu's equation
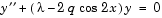
Because the unknown parameter 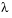 is present, this second-order differential equation is subject to three boundary conditions
is present, this second-order differential equation is subject to three boundary conditions
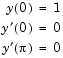
Note
The demo mat4bvp contains the complete code for this example. The demo uses subfunctions to place all functions required by bvp4c in a single M-file. To run this example type mat4bvp at the command line. See BVP Solver Basic Syntax for more information.
|
bvp4c, you must rewrite the equations as an equivalent system of first-order differential equations. Using a substitution 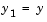 and
and 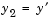 , the differential equation is written as a system of two first-order equations
, the differential equation is written as a system of two first-order equations
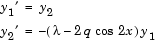
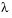 . The boundary conditions become
. The boundary conditions become
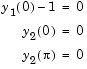
bvp4c can use. Because there is an unknown parameter, the function must be of the form
mat4ode.
See Finding Unknown Parameters for more information about using unknown parameters with bvp4c.
solinit with bvpinit, you need to provide initial guesses for both the solution and the unknown parameter.
mat4init provides an initial guess for the solution. mat4init uses 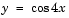 because this function satisfies the boundary conditions and has the correct qualitative behavior (the correct number of sign changes).
because this function satisfies the boundary conditions and has the correct qualitative behavior (the correct number of sign changes).
In the call to bvpinit, the third argument, lambda, provides an initial guess for the unknown parameter 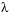 .
.
This example uses @ to pass mat4init as a function handle to bvpinit.
Note
See the function_handle (@), func2str, and str2func reference pages, and the Function Handles chapter of "Programming and Data Types" in the MATLAB documentation for information about function handles.
|
mat4bvp example calls bvp4c with the functions mat4ode and mat4bc and the structure solinit created with bvpinit.
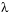 found by
found by bvp4c.
deval to evaluate the numerical solution at 100 equally spaced
points in the interval 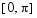 , and plot its first component. This component
approximates
, and plot its first component. This component
approximates 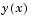 .
.
See Evaluating the Solution at Specific Points for information about using deval.
The following plot shows the eigenfunction associated with the final eigenvalue 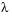 = 17.097.
= 17.097.
Finding Unknown Parameters
The bvp4c solver can find unknown parameters 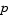 for problems of the form
for problems of the form
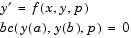
You must provide bvp4c an initial guess for any unknown parameters in the vector solinit.parameters. When you call bvpinit to create the structure solinit, specify the initial guess as a vector in the additional argument parameters.
The bvp4c function arguments odefun and bcfun must each have a third argument.
The bvp4c solver calculates intermediate values of unknown parameters at each iteration, and passes the latest values to odefun and bcfun in the parameters arguments. The solver returns the final values of these unknown parameters in sol.parameters. See Example: Mathieu's Equation.
Evaluating the Solution at Specific Points
The collocation method implemented in bvp4c produces a C1-continuous solution over the whole interval of integration 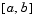 . You can evaluate the approximate solution,
. You can evaluate the approximate solution, 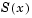 , at any point in
, at any point in 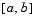 using the helper function
using the helper function deval and the structure sol returned by bvp4c.
The deval function is vectorized. For a vector xint, the ith column of Sxint approximates the solution  .
.
 | Boundary Value Problem Solver | Using Continuation to Make a Good Initial Guess |  |