

| Wavelet Toolbox |   |
Integrate wavelet function psi
Syntax
[INTEG,XVAL] = intwave('wname',PREC) [INTEG,XVAL] = intwave('wname',PREC,PFLAG) [INTEG,XVAL] = intwave('wname')
Description
[INTEG,XVAL] = intwave('wname',PREC) computes the integral, INTEG, of the wavelet function 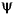 (from
(from 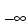 to
to XVAL values):
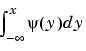 for x in
for x in XVAL.
The function 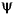 is approximated on the 2PREC points grid
is approximated on the 2PREC points grid XVAL where PREC is a positive integer. 'wname' is a string containing the name of the wavelet 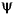 (see
(see wfilters for more information).
Output argument INTEG is a real or complex vector depending on the wavelet type.
[INTDEC,XVAL,INTREC] = intwave('wname',PREC) computes the integrals, INTDEC and INTREC, of the wavelet decomposition function 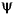 dec and the wavelet reconstruction function
dec and the wavelet reconstruction function 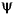 rec.
rec.
[INTEG,XVAL] = intwave('wname',PREC) is equivalent to [INTEG,XVAL] = intwave('wname',PREC,0).
[INTEG,XVAL] = intwave('wname') is equivalent to [INTEG,XVAL] = intwave('wname',8).
When used with three arguments intwave('wname',IN2,IN3), PREC = max(IN2,IN3) and plots are given.
When IN2 is equal to the special value 0, intwave('wname',0) is equivalent to intwave('wname',8,IN3).
intwave('wname') is equivalent to intwave('wname',8).
intwave is used only for continuous analysis (see cwt for more information).
Examples
% Set wavelet name. wname = 'db4'; % Plot wavelet function. [phi,psi,xval] = wavefun(wname,7); subplot(211); plot(xval,psi); title('Wavelet'); % Compute and plot wavelet integrals approximations % on a dyadic grid. [integ,xval] = intwave(wname,7); subplot(212); plot(xval,integ); title(['Wavelet integrals over [-Inf x] ' ... 'for each value of xval']);
Algorithm
First, the wavelet function is approximated on a grid of 2PREC points using wavefun. A piecewise constant interpolation is used to compute the integrals using cumsum.
See Also
wavefun
 | ind2depo | isnode |  |