Statistics Toolbox

Random Number Generator

The methods for generating random numbers from any distribution all start with uniform random numbers. Once you have a uniform random number generator, you can produce random numbers from other distributions either directly or by using inversion or rejection methods, described below. See Syntax for Random Number Functions for details on using generator functions.

Direct

Direct methods flow from the definition of the distribution.

As an example, consider generating binomial random numbers. You can think of binomial random numbers as the number of heads in n tosses of a coin with probability p of a heads on any toss. If you generate n uniform random numbers and count the number that are greater than p, the result is binomial with parameters n and p.

Inversion

The inversion method works due to a fundamental theorem that relates the uniform distribution to other continuous distributions.

If F is a continuous distribution with inverse F ^-1, and U is a uniform random number, then F ^-1(U) has distribution F.

So, you can generate a random number from a distribution by applying the inverse function for that distribution to a uniform random number. Unfortunately, this approach is usually not the most efficient.

Rejection

The functional form of some distributions makes it difficult or time consuming to generate random numbers using direct or inversion methods. Rejection methods can sometimes provide an elegant solution in these cases.

Suppose you want to generate random numbers from a distribution with pdf f. To use rejection methods you must first find another density, g, and a constant, c, so that the inequality below holds.

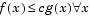
You then generate the random numbers you want using the following steps:

1. Generate a random number x from distribution G with density g.
2. Form the ratio
   
   .
3. Generate a uniform random number u.
4. If the product of u and r is less than one, return x.
5. Otherwise repeat steps one to three.

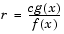For efficiency you need a cheap method for generating random numbers from G, and the scalar c should be small. The expected number of iterations is c.

Syntax for Random Number Functions

You can generate random numbers from each distribution. This function provides a single random number or a matrix of random numbers, depending on the arguments you specify in the function call.

For example, here is the way to generate random numbers from the beta distribution. Four statements obtain random numbers: the first returns a single number, the second returns a 2-by-2 matrix of random numbers, and the third and fourth return 2-by-3 matrices of random numbers.

• a = 1;
  b = 2;
  c = [.1 .5; 1 2];
  d = [.25 .75; 5 10];
  m = [2 3];
  nrow = 2;
  ncol = 3;
  r1 = betarnd(a,b)
  r1 =
      0.4469
  r2 = betarnd(c,d)
  r2 =
      0.8931    0.4832
      0.1316    0.2403
  r3 = betarnd(a,b,m)
  r3 =
      0.4196    0.6078    0.1392
      0.0410    0.0723    0.0782
  r4 = betarnd(a,b,nrow,ncol)
  r4 =
      0.0520    0.3975    0.1284
      0.3891    0.1848    0.5186
  

Inverse Cumulative Distribution Function

Mean and Variance as a Function of Parameters