Statistics Toolbox

Inverse Cumulative Distribution Function

The inverse cumulative distribution function returns critical values for hypothesis testing given significance probabilities. To understand the relationship between a continuous cdf and its inverse function, try the following:

• x = [-3:0.1:3];
  xnew = norminv(normcdf(x,0,1),0,1);
  

How does xnew compare with x? Conversely, try this:

• p = [0.1:0.1:0.9];
  pnew = normcdf(norminv(p,0,1),0,1);
  

How does pnew compare with p?

Calculating the cdf of values in the domain of a continuous distribution returns probabilities between zero and one. Applying the inverse cdf to these probabilities yields the original values.

For discrete distributions, the relationship between a cdf and its inverse function is more complicated. It is likely that there is no x value such that the cdf of x yields p. In these cases the inverse function returns the first value x such that the cdf of x equals or exceeds p. Try this:

• x = [0:10];
  y = binoinv(binocdf(x,10,0.5),10,0.5);
  

How does x compare with y?

The commands below illustrate the problem with reconstructing the probability p from the value x for discrete distributions.

• p = [0.1:0.2:0.9];
  pnew = binocdf(binoinv(p,10,0.5),10,0.5)
  pnew =
      0.1719    0.3770    0.6230    0.8281    0.9453
  

The inverse function is useful in hypothesis testing and production of confidence intervals. Here is the way to get a 99% confidence interval for a normally distributed sample.

• p = [0.005 0.995];
  x = norminv(p,0,1)
  x =
     -2.5758    2.5758
  

The variable x contains the values associated with the normal inverse function with parameters µ=0 and 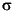=1 at the probabilities in p. The difference p(2)-p(1) is 0.99. Thus, the values in x define an interval that contains 99% of the standard normal probability.

The inverse function call has the same general format for every distribution in the Statistics Toolbox. The first input argument of every inverse function is the set of probabilities for which you want to evaluate the critical values. Other arguments contain as many parameters as are necessary to define the distribution uniquely.

Cumulative Distribution Function (cdf)

Random Number Generator