Statistics Toolbox

Example: One-Way ANOVA

The data below comes from a study by Hogg and Ledolter (1987) of bacteria counts in shipments of milk. The columns of the matrix hogg represent different shipments. The rows are bacteria counts from cartons of milk chosen randomly from each shipment. Do some shipments have higher counts than others?

• load hogg
  hogg
  hogg =
      24    14    11     7    19
      15     7     9     7    24
      21    12     7     4    19
      27    17    13     7    15
      33    14    12    12    10
      23    16    18    18    20
  [p,tbl,stats] = anova1(hogg);
  p
  p =
     1.1971e-04
  

The standard ANOVA table has columns for the sums of squares, degrees of freedom, mean squares (SS/df), F statistic, and p-value.

You can use the F statistic to do a hypothesis test to find out if the bacteria counts are the same. anova1 returns the p-value from this hypothesis test.

In this case the p-value is about 0.0001, a very small value. This is a strong indication that the bacteria counts from the different tankers are not the same. An F statistic as extreme as the observed F would occur by chance only once in 10,000 times if the counts were truly equal.

The p-value returned by anova1 depends on assumptions about the random disturbances 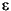_ij in the model equation. For the p-value to be correct, these disturbances need to be independent, normally distributed, and have constant variance. See Robust and Nonparametric Methods for a nonparametric function that does not require a normal assumption.

You can get some graphical assurance that the means are different by looking at the box plots in the second figure window displayed by anova1.

One-Way Analysis of Variance (ANOVA)

Multiple Comparisons