Statistics Toolbox

One-Way Analysis of Variance (ANOVA)

The purpose of one-way ANOVA is to find out whether data from several groups have a common mean. That is, to determine whether the groups are actually different in the measured characteristic.

One-way ANOVA is a simple special case of the linear model. The one-way ANOVA form of the model is

where:

• y_ij is a matrix of observations in which each column represents a different group.
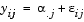
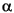• _.j is a matrix whose columns are the group means. (The "dot j" notation means that 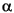applies to all rows of the jth column. That is, the value 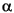_ij is the same for all i.)
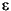• _ij is a matrix of random disturbances.

The model posits that the columns of y are a constant plus a random disturbance. You want to know if the constants are all the same.

The following sections explore one-way ANOVA in greater detail:

• Example: One-Way ANOVA
• Multiple Comparisons

Linear Models

Example: One-Way ANOVA