Using Simulink

Linearizing Models

Simulink provides the linmod and dlinmod functions to extract linear models in the form of the state-space matrices A, B, C, and D. State-space matrices describe the linear input-output relationship as

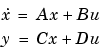
where x, u, and y are state, input, and output vectors, respectively. For example, the following model is called lmod.

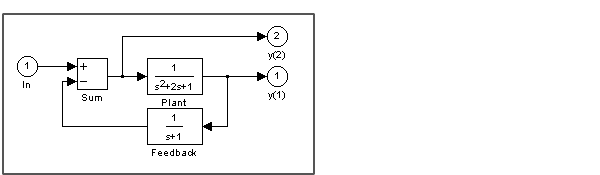
To extract the linear model of this Simulink system, enter this command.

• [A,B,C,D] = linmod('lmod')
  A =
     -2    -1    -1
      1     0     0
      0     1    -1
  B =
      1
      0
      0
  C =
      0     1     0
      0     0    -1
  D =
      0
      1
  

Inputs and outputs must be defined using Inport and Outport blocks from the Signals & Systems library. Source and sink blocks do not act as inputs and outputs. Inport blocks can be used in conjunction with source blocks, using a Sum block. Once the data is in the state-space form or converted to an LTI object, you can apply functions in the Control System Toolbox for further analysis:

• Conversion to an LTI object

• sys = ss(A,B,C,D);
  

• Bode phase and magnitude frequency plot

• bode(A,B,C,D) or bode(sys)
  

• Linearized time response

• step(A,B,C,D) or step(sys)
  impulse(A,B,C,D) or impulse(sys)
  lsim(A,B,C,D,u,t) or lsim(sys,u,t)
  

You can use other functions in the Control System Toolbox and Robust Control Toolbox for linear control system design.

When the model is nonlinear, an operating point can be chosen at which to extract the linearized model. The nonlinear model is also sensitive to the perturbation sizes at which the model is extracted. These must be selected to balance the tradeoff between truncation and roundoff error. Extra arguments to linmod specify the operating point and perturbation points.

• [A,B,C,D] = linmod('sys', x, u, pert, xpert, upert)
  

For discrete systems or mixed continuous and discrete systems, use the function dlinmod for linearization. This has the same calling syntax as linmod except that the second right-hand argument must contain a sample time at which to perform the linearization.

Using linmod to linearize a model that contains Derivative or Transport Delay blocks can be troublesome. Before linearizing, replace these blocks with specially designed blocks that avoid the problems. These blocks are in the Simulink Extras library in the Linearization sublibrary. You access the Extras library by opening the Blocksets & Toolboxes icon:

• For the Derivative block, use the Switched derivative for linearization.
• For the Transport Delay block, use the Switched transport delay for linearization. (Using this block requires that you have the Control System Toolbox.)

When using a Derivative block, you can also try to incorporate the derivative term in other blocks. For example, if you have a Derivative block in series with a Transfer Fcn block, it is better implemented (although this is not always possible) with a single Transfer Fcn block of the form

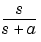
In this example, the blocks on the left of this figure can be replaced by the block on the right.

Viewing Output Trajectories

Finding Steady-State Points