

| Simulink Reference |   |
Extract the linear state-space model of a system around an operating point.
Syntax
Arguments
Description
linmod obtains linear models from systems of ordinary differential equations described as Simulink models. linmod returns the linear model in state-space form, A, B, C, D, which describes the linearized input-output relationship.
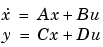
Inputs and outputs are denoted in Simulink block diagrams using Inport and Outport blocks.
[A,B,C,D] = linmod('sys', x, u) obtains the linearized model of sys around an operating point with the specified state variables x and the input u. If you omit x and u, the default values are zero.
[num,den] = linfun('sys', x, u) returns the linearized model in transfer function form.
sys_struc = linfun('sys', x, u) returns a structure that contains the linearized model, including state names, input and output names, and information about the operating point.
Discrete-Time System Linearization
The function dlinmod can linearize discrete, multirate, and hybrid continuous and discrete systems at any given sampling time. Use the same calling syntax for dlinmod as for linmod, but insert the sample time at which to perform the linearization as the second argument. For example,
produces a discrete state-space model at the sampling time Ts and the operating point given by the state vector x and input vector u. To obtain a continuous model approximation of a discrete system, set Ts to 0.
For systems composed of linear, multirate, discrete, and continuous blocks, dlinmod produces linear models having identical frequency and time responses (for constant inputs) at the converted sampling time Ts, provided that
For systems that do not meet the first condition, in general the linearization is a time-varying system, which cannot be represented with the [A,B,C,D] state-space model that dlinmod returns.
Computing the eigenvalues of the linearized matrix Ad provides an indication of the stability of the system. The system is stable if Ts>0 and the eigenvalues are within the unit circle, as determined by this statement:
Likewise, the system is stable if Ts = 0 and the eigenvalues are in the left half plane, as determined by this statement:
When the system is unstable and the sample time is not an integer multiple of the other sampling times, dlinmod produces Ad and Bd matrices, which can be complex. The eigenvalues of the Ad matrix in this case still, however, provide a good indication of stability.
You can use dlinmod to convert the sample times of a system to other values or to convert a linear discrete system to a continuous system or vice versa.
You can find the frequency response of a continuous or discrete system by using the bode command.
Notes
By default, the system time is set to zero. For systems that are dependent on time, you can set the variable pert to a two-element vector, where the second element is used to set the value of t at which to obtain the linear model.
The ordering of the states from the nonlinear model to the linear model is maintained. For Simulink systems, a string variable that contains the block name associated with each state can be obtained using
where xstring is a vector of strings whose ith row is the block name associated with the ith state. Inputs and outputs are numbered sequentially on the diagram.
For single-input multioutput systems, you can convert to transfer function form using the routine ss2tf or to zero-pole form using ss2zp. You can also convert the linearized models to LTI objects using ss. This function produces an LTI object in state-space form that can be further converted to transfer function or zero-pole-gain form using tf or zpk.
Linearizing a model that contains Derivative or Transport Delay blocks can be troublesome (see Linearizing Models).
 | Linearization and Trimming Commands | trim |  |