Simulink Reference

trim

Find a trim point of a dynamic system

Syntax

• [x,u,y,dx] = trim('sys')
  [x,u,y,dx] = trim('sys',x0,u0,y0)
  [x,u,y,dx] = trim('sys',x0,u0,y0,ix,iu,iy)
  [x,u,y,dx] = trim('sys',x0,u0,y0,ix,iu,iy,dx0,idx)
  [x,u,y,dx] = trim('sys',x0,u0,y0,ix,iu,iy,dx0,idx,options)
  [x,u,y,dx] = trim('sys',x0,u0,y0,ix,iu,iy,dx0,idx,options,t)
  [x,u,y,dx,options] = trim('sys',...)
  

Description

A trim point, also known as an equilibrium point, is a point in the parameter space of a dynamic system at which the system is in a steady state. For example, a trim point of an aircraft is a setting of its controls that causes the aircraft to fly straight and level. Mathematically, a trim point is a point where the system's state derivatives equal zero. trim starts from an initial point and searches, using a sequential quadratic programming algorithm, until it finds the nearest trim point. You must supply the initial point implicitly or explicitly. If trim cannot find a trim point, it returns the point encountered in its search where the state derivatives are closest to zero in a min-max sense; that is, it returns the point that minimizes the maximum deviation from zero of the derivatives. trim can find trim points that meet specific input, output, or state conditions, and it can find points where a system is changing in a specified manner, that is, points where the system's state derivatives equal specific nonzero values.

[x,u,y] = trim('sys') finds the equilibrium point nearest to the system's initial state, x0. Specifically, trim finds the equilibrium point that minimizes the maximum absolute value of [x-x0,u,y]. If trim cannot find an equilibrium point near the system's initial state, it returns the point at which the system is nearest to equilibrium. Specifically, it returns the point that minimizes
abs(dx-0). You can obtain x0 using this command.

• [sizes,x0,xstr] = sys([],[],[],0)
  

[x,u,y] = trim('sys',x0,u0,y0) finds the trim point nearest to x0, u0, y0, that is, the point that minimizes the maximum value of

• abs([x-x0; u-u0; y-y0])
  

The command

• trim('sys', x0, u0, y0, ix, iu, iy)
  

finds the trim point closest to x0, u0, y0 that satisfies a specified set of state, input, and/or output conditions. The integer vectors ix, iu, and iy select the values in x0, u0, and y0 that must be satisfied. If trim cannot find an equilibrium point that satisfies the specified set of conditions exactly, it returns the nearest point that satisfies the conditions, namely

• abs([x(ix)-x0(ix); u(iu)-u0(iu); y(iy)-y0(iy)])
  

Use the syntax

• [x,u,y,dx] = trim('sys', x0, u0, y0, ix, iu, iy, dx0, idx)
  

to find specific nonequilibrium points, that is, points at which the system's state derivatives have some specified nonzero value. Here, dx0 specifies the state derivative values at the search's starting point and idx selects the values in dx0 that the search must satisfy exactly.

The optional options argument is an array of optimization parameters that trim passes to the optimization function that it uses to find trim points. The optimization function, in turn, uses this array to control the optimization process and to return information about the process. trim returns the options array at the end of the search process. By exposing the underlying optimization process in this way, trim allows you to monitor and fine-tune the search for trim points.

Five of the optimization array elements are particularly useful for finding trim points. The following table describes how each element affects the search for a trim point.

No.	Default	Description
1	0	Specifies display options. 0 specifies no display; 1 specifies tabular output; -1 suppresses warning messages.
2	0.0001	Precision the computed trim point must attain to terminate the search.
3	0.0001	Precision the trim search goal function must attain to terminate the search.
4	0.0001	Precision the state derivatives must attain to terminate the search.
10	N/A	Returns the number of iterations used to find a trim point.

See the Optimization Toolbox User's Guide for a detailed description of the options array.

Examples

Consider a linear state-space model

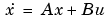
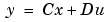
The A, B, C, and D matrices are as follows in a system called sys.

• A = [-0.09 -0.01;  1   0];
  B = [ 0    -7;     0  -2];
  C = [ 0     2;     1  -5];
  D = [-3     0;     1   0];
  

Example 1

To find an equilibrium point, use

• [x,u,y,dx,options] = trim('sys')
  x =
     0
     0
  u =
     0
  y =
     0
     0
  dx =
     0
     0
  

The number of iterations taken is

• options(10)
  ans =
        7
  

Example 2

To find an equilibrium point near x = [1;1], u = [1;1], enter

• x0 = [1;1];
  u0 = [1;1];
  [x,u,y,dx,options] = trim('sys', x0, u0);
  x =
      1.0e-11 *
     -0.1167
     -0.1167
  u =
      0.3333
      0.0000
  y =
     -1.0000
      0.3333
  dx =
      1.0e-11 *
      0.4214
      0.0003
  

The number of iterations taken is

• options(10)
  ans = 
        25
  

Example 3

To find an equilibrium point with the outputs fixed to 1, use

• y = [1;1];
  iy = [1;2];
  [x,u,y,dx] = trim('sys', [], [], y, [], [], iy)
  x =
      0.0009
     -0.3075
  u =
     -0.5383
      0.0004
  y =
      1.0000
      1.0000
  dx =
      1.0e-16 *
     -0.0173
      0.2396
  

Example 4

To find an equilibrium point with the outputs fixed to 1 and the derivatives set to 0 and 1, use

• y = [1;1];
  iy = [1;2];
  dx = [0;1];
  idx = [1;2];
  [x,u,y,dx,options] = trim('sys',[],[],y,[],[],iy,dx,idx)
  x =
      0.9752
     -0.0827
  u =
     -0.3884
     -0.0124
  y =
      1.0000
      1.0000
  dx =
      0.0000
      1.0000
  

The number of iterations taken is

• options(10)
  ans = 
        13
  

Limitations

The trim point found by trim starting from any given initial point is only a local value. Other, more suitable trim points may exist. Thus, if you want to find the most suitable trim point for a particular application, it is important to try a number of initial guesses for x, u, and y.

Algorithm

trim uses a sequential quadratic programming algorithm to find trim points. See the documentation for the Optimization Toolbox for a description of this algorithm.

linmod, dlinmod, linmod2

Model Construction Commands