cohere (Signal Processing Toolbox)

Estimate magnitude squared coherence function between two signals

Syntax

Cxy = cohere(x,y)
Cxy = cohere(x,y,nfft)
[Cxy,f] = cohere(x,y,nfft,fs)
Cxy = cohere(x,y,nfft,fs,window)
Cxy = cohere(x,y,nfft,fs,window,numoverlap)
Cxy = cohere(x,y,...,'dflag')
cohere(x,y)

Description

Cxy = cohere(x,y) finds the magnitude squared coherence between length n signal vectors x and y. The coherence is a function of the power spectra of x and y and the cross spectrum of x and y.

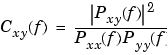
x and y must be the same length.

nfft specifies the FFT length that cohere uses. This value determines the frequencies at which the coherence is estimated. fs is a scalar that specifies the sampling frequency. window specifies a windowing function and the number of samples cohere uses in its sectioning of the x and y vectors. numoverlap is the number of samples by which the window sections overlap for both x and y. Any arguments that you omit from the end of the parameter list use the default values shown below.

Cxy = cohere(x,y) uses the following default values:

nfft = min(256,length(x))
fs = 2
window is a periodic Hanning window of length nfft.
numoverlap = 0

If x is real, cohere estimates the coherence function at positive frequencies only; in this case, the output Cxy is a column vector of length nfft/2 + 1 for nfft even and (nfft + 1)/2 for n odd. If x or y is complex, cohere estimates the coherence function at both positive and negative frequencies, and Cxy has length nfft.

Cxy = cohere(x,y,nfft) uses the FFT length nfft in estimating the power spectrum for x. Specify nfft as a power of 2 for fastest execution.

[Cxy,f] = cohere(x,y,nfft,fs) returns a vector f of frequencies at which the function evaluates the coherence. fs is the sampling frequency. f is the same size as Cxy, so plot(f,Cxy) plots the coherence function versus properly scaled frequency. fs has no effect on the output Cxy; it is a frequency scaling multiplier.

cohere(x,y,nfft,fs,window) specifies a windowing function and the number of samples per section of the vectors x and y. If you supply a scalar for window, cohere uses a Hanning window of that length. The length of the window must be less than or equal to nfft; cohere zero pads the sections if the window length exceeds nfft.

cohere(x,y,nfft,fs,window,numoverlap) overlaps the sections of x and y by numoverlap samples.

Note If you use cohere on two linearly related signals [1] with a single, non-overlapping window, the output for all frequencies is Cxy = 1.

You can use the empty matrix [] to specify the default value for any input argument except x or y. For example:

```
cohere(x,y,[],[],kaiser(128,5));
```

uses 256 as the value for nfft and 2 as the value for fs.

cohere(x,y,...,'dflag') specifies a detrend option, where 'dflag' is:

'linear', to remove the best straight-line fit from the prewindowed sections of x and y
'mean', to remove the mean from the prewindowed sections of x and y
'none', for no detrending (default)

The 'dflag' parameter must appear last in the list of input arguments. cohere recognizes a 'dflag' string no matter how many intermediate arguments are omitted.

cohere with no output arguments plots the coherence estimate versus frequency in the current figure window.

Examples

Compute and plot the coherence estimate between two colored noise sequences x and y:

randn('state',0);
h = fir1(30,0.2,rectwin(31));
h1 = ones(1,10)/sqrt(10);
r = randn(16384,1);
x = filter(h1,1,r);
y = filter(h,1,x);
cohere(x,y,1024,[],[],512)

Diagnostics

An appropriate diagnostic message is displayed when incorrect arguments are used:

Requires window's length to be no greater than the FFT length.
Requires NOVERLAP to be strictly less than the window length.
Requires positive integer values for NFFT and NOVERLAP.
Requires vector (either row or column) input.
Requires inputs X and Y to have the same length.

Algorithm

cohere estimates the magnitude squared coherence function [2] using Welch's method of power spectrum estimation (see references [3] and [4]), as follows:

It divides the signals x and y into separate overlapping sections, detrends each section, and multiplies each section by window.
It calculates the length nfft fast Fourier transform of each section.
It averages the squares of the spectra of the x sections to form Pxx, averages the squares of the spectra of the y sections to form Pyy, and averages the products of the spectra of the x and y sections to form Pxy. It calculates Cxy by the following formula.

```
Cxy = abs(Pxy).^2/(Pxx.*Pyy)
```

See Also

csd, pwelch, tfe

References

[1] Stoica, P., and R. Moses. Introduction to Spectral Analysis. Upper Saddle River, NJ: Prentice-Hall, 1997. Pgs. 61-64.

[2] Kay, S.M. Modern Spectral Estimation. Englewood Cliffs, NJ: Prentice-Hall, 1988. Pg. 454.

[3] Rabiner, L.R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975.

[4] Welch, P.D. "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms." IEEE Trans. Audio Electroacoust. Vol. AU-15 (June 1967). Pgs. 70-73.

chirp conv