chirp (Signal Processing Toolbox)

Generate a swept-frequency cosine

Syntax

y = chirp(t,f0,t1,f1)
y = chirp(t,f0,t1,f1,'method')
y = chirp(t,f0,t1,f1,'method',phi)
y = chirp(t,f0,t1,f1,'quadratic',phi,'shape')

Description

y = chirp(t,f0,t1,f1) generates samples of a linear swept-frequency cosine signal at the time instances defined in array t, where f0 is the instantaneous frequency at time 0, and f1 is the instantaneous frequency at time t1. f0 and f1 are both in hertz. If unspecified, f0 is 0, t1 is 1, and f1 is 100.

Y = CHIRP(T,F0,T1,F1,'method') specifies alternative sweep method options, where method can be:

linear, which specifies an instantaneous frequency sweep f_i(t) given by

where

ensures that the desired frequency breakpoint f₁ at time t₁ is maintained.

quadratic, which specifies an instantaneous frequency sweep f_i(t) given by

where

If f₀ > f₁ (downsweep), the default shape is convex. If f₀< f₁ (upsweep), the default shape is concave.

logarithmic specifies an instantaneous frequency sweep f_i(t) given by

where

For a log-sweep, f1 must be greater than f0.

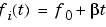
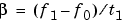
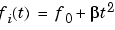
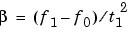
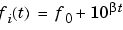
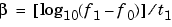
Each of the above methods can be entered as 'li', 'q', and 'lo', respectively.

y = chirp(t,f0,t1,f1,'method',phi) allows an initial phase phi to be specified in degrees. If unspecified, phi is 0. Default values are substituted for empty or omitted trailing input arguments.

y = chirp(t,f0,t1,f1,'quadratic',phi,'shape') specifies the shape of the quadratic swept-frequency signal's spectrogram. shape is either concave or convex, which describes the shape of the parabola in the positive frequency axis. If shape is omitted, the default is convex for downsweep (f₀ > f₁) and is concave for upsweep (f₀< f₁).

Examples

Example 1

Compute the spectrogram of a chirp with linear instantaneous frequency deviation:

t = 0:0.001:2;              % 2 secs @ 1kHz sample rate
y = chirp(t,0,1,150);       % Start @ DC, cross 150Hz at t=1 sec
specgram(y,256,1e3,256,250) % Display the spectrogram

Example 2

Compute the spectrogram of a chirp with quadratic instantaneous frequency deviation:

t = -2:0.001:2;                     % ±2 secs @ 1kHz sample rate
y = chirp(t,100,1,200,'quadratic'); % Start @ 100Hz, cross 200Hz 
                                    %   at t=1 sec
specgram(y,128,1e3,128,120)         % Display the spectrogram

Example 3

Compute the spectrogram of a convex quadratic chirp:

t= -1:0.001:1;                    % +/-1 second @ 1kHz sample rate
fo=100; f1=400;                   % Start at 100Hz, go up to 400Hz
y=chirp(t,fo,1,f1,'q',[],'convex');
specgram(y,256,1000)              % Display the spectrogram.

Example 4

Compute the spectrogram of a concave quadratic chirp:

t= 0:0.001:1;                     % 1 second @ 1kHz sample rate
fo=100; f1=25;                    % Start at 100Hz, go down to 25Hz
y=chirp(t,fo,1,f1,'q',[],'concave');
specgram(y,256,1000)              % Display the spectrogram.

See Also

cos, diric, gauspuls, pulstran, rectpuls, sawtooth, sin, sinc, square, tripuls

cheby2 cohere