linprog (Optimization Toolbox)

Solve a linear programming problem

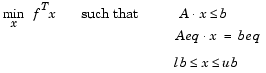
where f, x, b, beq, lb, and ub are vectors and A and Aeq are matrices.

Syntax

x = linprog(f,A,b,Aeq,beq)
x = linprog(f,A,b,Aeq,beq,lb,ub)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0)
x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval] = linprog(...)
[x,fval,exitflag] = linprog(...)
[x,fval,exitflag,output] = linprog(...)
[x,fval,exitflag,output,lambda] = linprog(...)

Description

linprog solves linear programming problems.

x = linprog(f,A,b) solves min f'*x such that A*x <= b.

x = linprog(f,A,b,Aeq,beq) solves the problem above while additionally satisfying the equality constraints Aeq*x = beq. Set A=[] and b=[] if no inequalities exist.

x = linprog(f,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables, x, so that the solution is always in the range lb <= x <= ub. Set Aeq=[] and beq=[] if no equalities exist.

x = linprog(f,A,b,Aeq,beq,lb,ub,x0) sets the starting point to x0. This option is only available with the medium-scale algorithm (the LargeScale parameter is set to 'off' using optimset). The default large-scale algorithm ignores any starting point.

x = linprog(f,A,b,Aeq,beq,lb,ub,x0,options) minimizes with the optimization parameters specified in the structure options. Use optimset to set these parameters.

[x,fval] = linprog(...) returns the value of the objective function fun at the solution x: fval = f'*x.

[x,lambda,exitflag] = linprog(...) returns a value exitflag that describes the exit condition.

[x,lambda,exitflag,output] = linprog(...) returns a structure output that contains information about the optimization.

[x,fval,exitflag,output,lambda] = linprog(...) returns a structure lambda whose fields contain the Lagrange multipliers at the solution x.

Input Arguments

Function Arguments contains general descriptions of arguments passed in to linprog. Options provides the function-specific details for the options parameters.

Output Arguments

Function Arguments contains general descriptions of arguments returned by linprog. This section provides function-specific details for exitflag, lambda, and output:

exitflag
Describes the exit condition:

> 0
The function converged to a solution x.

0
The maximum number of function evaluations or iterations was exceeded.

< 0
The function did not converge to a solution.

lambda
Structure containing the Lagrange multipliers at the solution x (separated by constraint type). The fields of the structure are:

lower
Lower bounds lb

upper
Upper bounds ub

ineqlin
Linear inequalities

eqlin
Linear equalities

output
Structure containing information about the optimization. The fields of the structure are:

iterations
Number of iterations taken.

algorithm
Algorithm used.

cgiterations
The number of PCG iterations (large-scale algorithm only).

`exitflag`	Describes the exit condition:
	> 0	The function converged to a solution `x`.
	0	The maximum number of function evaluations or iterations was exceeded.
	< 0	The function did not converge to a solution.
`lambda`	Structure containing the Lagrange multipliers at the solution `x` (separated by constraint type). The fields of the structure are:
	`lower`	Lower bounds `lb`
	`upper`	Upper bounds `ub`
	`ineqlin`	Linear inequalities
	`eqlin`	Linear equalities
`output`	Structure containing information about the optimization. The fields of the structure are:
	`iterations`	Number of iterations taken.
	`algorithm`	Algorithm used.
	`cgiterations`	The number of PCG iterations (large-scale algorithm only).

Options

Optimization options parameters used by linprog. Some parameters apply to all algorithms, and others are only relevant when using the large-scale algorithm.You can use optimset to set or change the values of these fields in the parameters structure, options. See Optimization Parameters, for detailed information.:

LargeScale
Use large-scale algorithm when set to 'on'. Use medium-scale algorithm when set to 'off'.

`LargeScale`	Use large-scale algorithm when set to `'on'`. Use medium-scale algorithm when set to `'off'`.

Medium-Scale and Large-Scale Algorithms. These parameters are used by both the medium-scale and large-scale algorithms:

Diagnostics
Print diagnostic information about the function to be minimized.

Display
Level of display. 'off' displays no output; 'iter' displays output at each iteration; 'final' (default) displays just the final output. At this time, the 'iter' level only works with the large-scale algorithm.

MaxIter
Maximum number of iterations allowed.

`Diagnostics`	Print diagnostic information about the function to be minimized.
`Display`	Level of display. `'off'` displays no output; `'iter'` displays output at each iteration; `'final'` (default) displays just the final output. At this time, the `'iter'` level only works with the large-scale algorithm.
`MaxIter`	Maximum number of iterations allowed.

Large-Scale Algorithm Only. These parameters are used only by the large-scale algorithm:

TolFun
Termination tolerance on the function value.

`TolFun`	Termination tolerance on the function value.

Examples

Find x that minimizes

subject to

First, enter the coefficients

f = [-5; -4; -6]
A =  [1 -1  1
      3  2  4
      3  2  0];
b = [20; 42; 30];
lb = zeros(3,1);

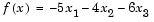
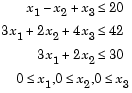
Next, call a linear programming routine.

[x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);

Entering x, lambda.ineqlin, and lambda.lower gets

x = 
     0.0000
    15.0000
     3.0000
lambda.ineqlin =
     0
     1.5000
     0.5000
lambda.lower =
     1.0000
     0
     0

Nonzero elements of the vectors in the fields of lambda indicate active constraints at the solution. In this case, the second and third inequality constraints (in lambda.ineqlin) and the first lower bound constraint (in lambda.lower) are active constraints (i.e., the solution is on their constraint boundaries).

Algorithm

Large-Scale Optimization. The large-scale method is based on LIPSOL (Linear Interior Point Solver, [3]), which is a variant of Mehrotra's predictor-corrector algorithm ([2]), a primal-dual interior-point method. A number of preprocessing steps occur before the algorithm begins to iterate. See Large-Scale Linear Programming.

Medium-Scale Optimization. linprog uses a projection method as used in the quadprog algorithm. linprog is an active set method and is thus a variation of the well-known simplex method for linear programming [1]. It finds an initial feasible solution by first solving another linear programming problem.

Diagnostics

Large-Scale Optimization. The first stage of the algorithm may involve some preprocessing of the constraints (see Large-Scale Linear Programming). Several possible conditions might occur that cause linprog to exit with an infeasibility message. In each case, the exitflag argument returned by linprog is set to a negative value to indicate failure.

If a row of all zeros is detected in Aeq but the corresponding element of beq is not zero, the exit message is

Exiting due to infeasibility:   An all zero row in the constraint 
matrix does not have a zero in corresponding right-hand size 
entry.

If one of the elements of x is found to not be bounded below, the exit message is

Exiting due to infeasibility:   Objective f'*x is unbounded below.

If one of the rows of Aeq has only one nonzero element, the associated value in x is called a singleton variable. In this case, the value of that component of x can be computed from Aeq and beq. If the value computed violates another constraint, the exit message is

Exiting due to infeasibility: Singleton variables in equality 
constraints are not feasible.

If the singleton variable can be solved for but the solution violates the upper or lower bounds, the exit message is

Exiting due to infeasibility: Singleton variables in the equality 
constraints are not within bounds.

Note The preprocessing steps are cumulative. For example, even if your constraint matrix does not have a row of all zeros to begin with, other preprocessing steps may cause such a row to occur.

Once the preprocessing has finished, the iterative part algorithm begins until the stopping criteria is met. (See Large-Scale Linear Programming for more information about residuals, the primal problem, the dual problem, and the related stopping criteria.) If the residuals are growing instead of getting smaller, or the residuals are neither growing nor shrinking, one of the two following termination messages displays, respectively,

One or more of the residuals, duality gap, or total relative error 
has grown 100000 times greater than its minimum value so far:

One or more of the residuals, duality gap, or total relative error 
has stalled:

After one of these messages displays, it is followed by one of the following six messages indicating if it appears that the dual, the primal, or both are infeasible. The messages differ according to how the infeasibility or unboundedness was measured.

The dual appears to be infeasible (and the primal unbounded).(The 
primal residual < TolFun.)

The primal appears to be infeasible (and the dual unbounded). (The 
dual residual < TolFun.)

The dual appears to be infeasible (and the primal unbounded) since 
the dual residual > sqrt(TolFun).(The primal residual < 
10*TolFun.)

The primal appears to be infeasible (and the dual unbounded) since 
the primal residual > sqrt(TolFun).(The dual residual < 
10*TolFun.)

The dual appears to be infeasible and the primal unbounded since 
the primal objective < -1e+10 and the dual objective < 1e+6.

The primal appears to be infeasible and the dual unbounded since 
the dual objective > 1e+10 and the primal objective > -1e+6.

Both the primal and the dual appear to be infeasible.

Note that, for example, the primal (objective) can be unbounded and the primal residual, which is a measure of primal constraint satisfaction, can be small.

Medium-Scale Optimization. linprog gives a warning when the solution is infeasible.

Warning: The constraints are overly stringent;
there is no feasible solution.

In this case, linprog produces a result that minimizes the worst case constraint violation.

When the equality constraints are inconsistent, linprog gives

Warning: The equality constraints are overly
stringent; there is no feasible solution.

Unbounded solutions result in the warning

Warning: The solution is unbounded and at infinity;
the constraints are not restrictive enough.

In this case, linprog returns a value of x that satisfies the constraints.

Limitations

Medium-Scale Optimization. At this time, the only levels of display, using the Display parameter in options, are 'off' and 'final'; iterative output using 'iter' is not available.

See Also

quadprog

References

[1] Dantzig, G.B., A. Orden, and P. Wolfe, "Generalized Simplex Method for Minimizing a Linear from Under Linear Inequality Constraints," Pacific Journal Math. Vol. 5, pp. 183-195.

[2] Mehrotra, S., "On the Implementation of a Primal-Dual Interior Point Method," SIAM Journal on Optimization, Vol. 2, pp. 575-601, 1992.

[3] Zhang, Y., "Solving Large-Scale Linear Programs by Interior-Point Methods Under the MATLAB Environment," Technical Report TR96-01, Department of Mathematics and Statistics, University of Maryland, Baltimore County, Baltimore, MD, July 1995.

gangstr lsqcurvefit