| System Identification Toolbox | |
Transform a model to state-space form.
Syntax
Description
m is the model given as any idmodel object. A, B, C, D,K, and X0 are the matrices in the state-space description
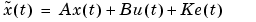
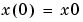
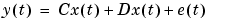
where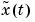 
is 
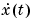or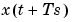 
depending on whether m is a continuous or discrete-time model.
dA, dB, dC, dD, dK, and dX0 are the standard deviations of the state-space matrices.
If the underlying model itself is a state-space model, the matrices correspond to the same basis. If the underlying model is an input-output model, an observer canonical form representation is obtained.
For a time-series model (no measured input channels, u= [ ]), B and D are returned as the empty matrices.
Subreferencing models in usual way (see idmodel properties) will give the state-space representation of the chosen channels. Notice in particular that
gives the response from the measured inputs. This is a model without a disturbance description. Moreover
('n' as in "noise") gives the disturbance description, i.e, a time-series description of the additive noise with no measured inputs, so that B=[] and D=[].
To obtain state-space descriptions that treat all input channels, both u and e as measured inputs, first apply the conversion
where the latter case first normalizes e to v, where v has a unit covariance matrix. See the reference page for noisecnv.
Algorithm
The computation of the standard deviations in the input-output case assumes that an A polynomial is not used together with a F or D polynomial in (Equation 3-43). For the computation of standard deviations in the case that the state-space parameters are complicated functions of the parameters, Gauss approximation formula is used together with numerical derivatives. The step-sizes for this differentiation are determined by nuderst.
See Also
| | ss, tf, zpk, frd | step | |