Tutorial (System Identification Toolbox)

System Identification Toolbox

Residual Analysis

The residuals associated with the data and a given model, as in (3-38), are ideally white and independent of the input for the model to correctly describe the system. The function

```
resid(Model,Data)
```

computes the residuals (prediction errors) e from the model when applied to Data, and performs whiteness and independence analyses. The auto correlation function of e and the cross-correlation function between e and u are computed and displayed for up to lag 25. Also displayed are 99% confidence intervals for these variables, assuming that e is indeed white and independent of u.

The rule is that if the correlation functions go significantly outside these confidence intervals, do not accept the corresponding model as a good description of the system. Some qualifications of this statement are necessary:

Model structures like the OE structure (3-17) and methods like the IV method (3-41) focus on the dynamics G and less about the disturbance properties H. If you are interested primarily in G, focus on the independence of e and u rather than the whiteness of e.
Correlation between e and u for negative lags, or current 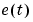affecting future 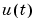, is an indication of output feedback. This is not a reason to reject the model. Correlation at negative lags is of interest, since certain methods do not work well when feedback is present in the input-output data, (see Feedback in Data), but concentrate on the positive lags in the cross-correlation plot for model validation purposes.
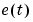When using the ARX model (3-14), the least squares procedure automatically makes the correlation between and 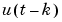zero for 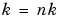, , 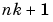, 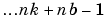for the data used for the estimation.

The residuals e together with the input u are returned by

```
E= resid(Model,Data)
```

as an iddata object. As part of the validation process, you can graph the residuals using

```
 plot(E)
```

for a simple visual inspection of irregularities and outliers. (See also Outliers and Bad Data; Multi-Experiment Data.)

Checking Pole-Zero Cancellations Model Error Models