System Identification Toolbox

General Polynomial Black-Box Models

Based on the prediction error method (3-38), you can construct models of basically any structure. For the general model (3-19), there is the function

• m = pem(Data,nn)
  

where nn gives all the orders and delays.

• nn = [na nb nc nd nf nk]
  

The nonzero orders of the model can also be defined as property name/property value pairs as in

• m = pem(Data,'na',na,'nb',nb,'nc',nc,'nk',nk)
  

The input parameters are defined in Polynomial Representation of Transfer Functions. The pem command covers all cases of black-box linear system models. For the common special cases

• m = armax(Data,[na nb nc nk])
  m = oe(Data,[nb nf nk])
  m = bj(Data,[nb nc nd nf nk])
  

can be used. These handle the model structures (3-16), (3-17) and (3-18), respectively.

All the routines also cover single-output, multi-input systems of the type

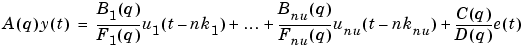
(3-41)

where nb, nf, and nk are row vectors of the same lengths as the number of input channels containing each of the orders and delays

• nb = [nb1 ...  nbnu];
  nf = [nf1 ...  nfnu];
  nk = [nk1 ...  nknu];
  

These parameter estimation routines require an iterative search for the minimum of the function (3-39). This search uses a special start-up procedure based on least squares and instrumental variables (the details are given as Equation (10.79) in Ljung (1999)). From the initial estimate, a Gauss-Newton minimization procedure is carried out until the norm of the Gauss-Newton direction is less than a certain tolerance. See Ljung (1999), Section 11.2 or Dennis and Schnabel(1983) for details. See also the entry at the end of this section on optional variables associated with the search.

The estimation routines also return the estimated covariance matrix of the estimated parameter vector as part of m. This reflects the reliability of the estimates. The covariance matrix estimate is computed under the assumption that it is possible to obtain a "true" description in the given structure.

The routines pem, armax, oe, and bj can also be started at any initial value mi that is a model object by replacing nn by mi. For example,

• m = pem(Data,mi)
  

While the search is typically initialized using the built-in start-up procedure giving just orders and delays (as described above), the ability to force a specific initial condition is useful in several contexts. Some examples are mentioned in Initial Parameter Values.

Information about how the minimization progresses can be supplied to the MATLAB command window by the property trace. See the list at the end of this section.

AR Models

State-Space Models