| System Identification Toolbox | |
Direct Estimation of the Frequency Response
The frequency response of a linear system is the Fourier transform of its impulse response. This description of the system gives considerable engineering insight into its properties. The relation between input and output is often written
where G is the transfer function and v is the additive disturbance. The function
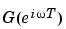
as a function of (angular) frequency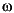 
is then the frequency response or frequency function. T is the sampling interval. If you need more details on the different interpretations of the frequency response, See "The System Identification Problem in the Tutorial chapter or any textbook on linear systems.
The system's frequency response is directly estimated using spectral analysis by the menu item Estimate > Spectral Model, and then selecting the Estimate button in the dialog box that opens. The result is placed on the Model Board under the default name spad. The best way to examine it is to plot it using the Model View Frequency Response. This view offers a number of different options on how to graph the curves. The frequencies for which to estimate the response can also be selected as an option under the Options menu in this View window.
The Spectral Analysis command also estimates the spectrum of the additive disturbance v(t) in the system description. This estimated disturbance spectrum is examined under the Model View item Noise Spectrum.
The Spectral Analysis estimate is stored as an idfrd object. If you need to further work with the estimates, you can export the model to the MATLAB workspace and retrieve the responses directly from this object or by Nyquist and Bode. See idfrd, bode, and nyquist in the "Command Reference" chapter for more information. (A model is exported by dragging and dropping it over the To Workspace icon.)
Two options that affect the spectral analysis estimate can be set in the dialog box. The most important choice is a number, M, (the size of the lag window) that affects the frequency resolution of the estimates. Essentially, the frequency resolution is about 2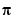
/M radians/(sampling interval). The choice of M is a trade-off between frequency resolution and variance (fluctuations). A large value of M gives good resolution but fluctuating and less reliable estimates. The default choice of M is good for systems that do not have very sharp resonances and may have to be adjusted for more resonant systems.
The options also offer a choice between the Blackman-Tukey windowing method spa (which is default) and a method based on smoothing direct Fourier transforms, etfe. etfe has an advantage for highly resonant systems, in that it is more efficient for large values of M. It however has the drawbacks that it requires linearly spaced frequency values, does not estimate the disturbance spectrum, and does not provide confidence intervals. The actual methods are described in more detail in the "Command Reference" chapter under spa and etfe. To obtain the spectral analysis model for the current settings of the options, you can just type the hotkey s in the ident window.
| | Direct Estimation of the Impulse Response | Estimation of Parametric Models | |