Fixed-Point Blockset

Addition

Consider the addition of two real-world values:

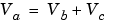
These values are represented by the general [Slope Bias] encoding scheme described in Scaling:

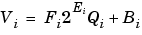
In a fixed-point system, the addition of values results in finding the variable Q_a:

This formula shows

• In general, Q_a is not computed through a simple addition of Q_b and Q_c.
• In general, there are two multiplies of a constant and a variable, two additions, and some additional bit shifting.

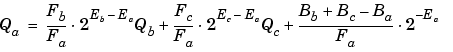
Inherited Scaling for Speed

In the process of finding the scaling of the sum, one reasonable goal is to simplify the calculations. Simplifying the calculations should reduce the number of operations thereby increasing execution speed. The following choices can help to minimize the number of arithmetic operations:

• Set B_a = B_b + B_c. This eliminates one addition.
• Set F_a = F_b or F_a = F_c. Either choice eliminates one of the two constant times variable multiplies.

The resulting formula is

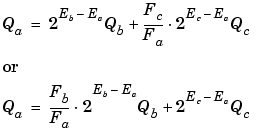
These equations appear to be equivalent. However, your choice of rounding and precision may make one choice stand out over the other. To further simplify matters, you could choose E_a = E_c or E_a = E_b. This will eliminate some bit shifting.

Inherited Scaling for Maximum Precision

In the process of finding the scaling of the sum, one reasonable goal is maximum precision. You can determine the maximum precision scaling if the range of the variable is known. Example: Maximizing Precision shows that you can determine the range of a fixed-point operation from 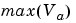and 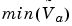. For a summation, you can determine the range from

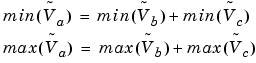
You can now derive the maximum precision slope:

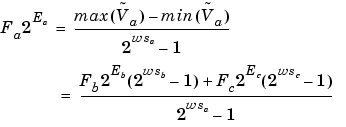
In most cases the input and output word sizes are much greater than one, and the slope becomes

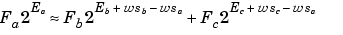
which depends only on the size of the input and output words. The corresponding bias is

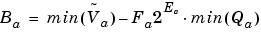
The value of the bias depends on whether the inputs and output are signed or unsigned numbers.

If the inputs and output are all unsigned, then the minimum value for these variables are all zero and the bias reduces to a particularly simple form:

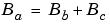
If the inputs and the output are all signed, then the bias becomes

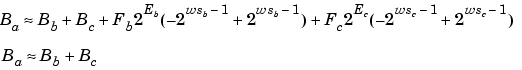
Radix Point-Only Scaling

For radix point-only scaling, finding Q_a results in this simple expression:

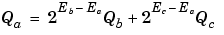
This scaling choice results in only one addition and some bit shifting. The avoidance of any multiplications is a big advantage of radix point-only scaling.

Note    The subtraction of values produces results that are analogous to those produced by the addition of values.

Recommendations for Arithmetic and Scaling

Accumulation