Fixed-Point Blockset

Scaling

The dynamic range of fixed-point numbers is much less than that of floating-point numbers with equivalent word sizes. To avoid overflow conditions and minimize quantization errors, fixed-point numbers must be scaled.

With the Fixed-Point Blockset, you can select a fixed-point data type whose scaling is defined by its default radix point, or you can select a generalized fixed-point data type and choose an arbitrary linear scaling that suits your needs. This section presents the scaling choices available for generalized fixed-point data types.

A fixed-point number can be represented by a general [Slope Bias] encoding scheme

where

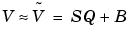
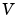• is an arbitrarily precise real-world value.
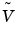• is the approximate real-world value.
• Q is an integer that encodes V.
• S = F.2^E is the slope.
• B is the bias.

The slope is partitioned into two components:

• 2^E specifies the radix point. E is the fixed power-of-two exponent.
• F is the fractional slope. It is normalized such that .

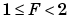Note    S and B are constants and do not show up in the computer hardware directly - only the quantization value Q is stored in computer memory.

The scaling modes available to you within this encoding scheme are described below. For detailed information about how the supported scaling modes effect fixed-point operations, refer to Recommendations for Arithmetic and Scaling.

Radix Point-Only Scaling

As the name implies, radix point-only (or "powers-of-two") scaling involves moving only the radix point within the generalized fixed-point word. The advantage of this scaling mode is the number of processor arithmetic operations is minimized.

With radix point-only scaling, the components of the general [Slope Bias] formula have these values:

• F = 1
• S = 2^E
• B = 0

That is, the scaling of the quantized real-world number is defined only by the slope S, which is restricted to a power of two.

In the Fixed-Point Blockset, you specify radix point-only scaling with the syntax 2^-E where E is unrestricted. This creates a MATLAB structure with a bias B = 0 and a fractional slope F = 1.0. For example, the syntax 2^-10 defines a scaling such that the radix point is at a location 10 places to the left of the least significant bit.

[Slope Bias] Scaling

When you scale by slope and bias, the slope S and bias B of the quantized real-world number can take on any value. You specify scaling by slope and bias with the syntax [slope bias], which creates a MATLAB structure with the given slope and bias. For example, a [Slope Bias] scaling specified by [5/9 10] defines a slope of 5/9 and a bias of 10. The slope must be a positive number.

See Example: Fixed-Point Scaling and Example: Constant Scaling for Best Precision for more information.

Radix Point Interpretation

Quantization