Fixed-Point Blockset

Example: Maximizing Precision

Precision is limited by slope. To achieve maximum precision, you should make the slope as small as possible while keeping the range adequately large. The bias is adjusted in coordination with the slope.

Assume the maximum and minimum real-world value is given by max(V) and min(V), respectively. These limits may be known based on physical principles or engineering considerations. To maximize the precision, you must decide upon a rounding scheme and whether overflows saturate or wrap. To simplify matters, this example assumes the minimum real-world value corresponds to the minimum encoded value, and the maximum real-world value corresponds to the maximum encoded value. Using the encoding scheme described in Scaling, these values are given by

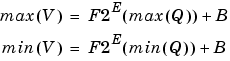
Solving for the slope, you get

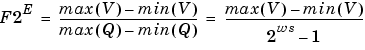
This formula is independent of rounding and overflow issues, and depends only on the word size, ws.

Example: Limitations on Precision and Errors

Limitations on Range