Fixed-Point Blockset

Range and Precision

The range of a number gives the limits of the representation while the precision gives the distance between successive numbers in the representation. The range and precision of an IEEE floating-point number depend on the specific format.

Range

The range of representable numbers for an IEEE floating-point number with f bits allocated for the fraction, e bits allocated for the exponent, and the bias of e given by bias = 2^{e - 1}- 1 is given below.

where

• Normalized positive numbers are defined within the range 2^{1 - bias} to
  (2 - 2^-f).2^bias.
• Normalized negative numbers are defined within the range -2^{1 - bias} to
  -(2 - 2^-f).2^bias.
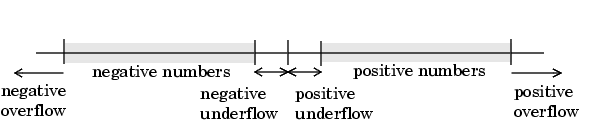
• Positive numbers greater than (2 - 2^-f).2^bias, and negative numbers greater than -(2 - 2^-f).2^bias are overflows.
• Positive numbers less than 2^{1 - bias}, and negative numbers less than -2^{1 - bias} are either underflows or denormalized numbers.
• Zero is given by a special bit pattern, where e = 0 and f = 0.

Overflows and underflows result from exceptional arithmetic conditions. Floating-point numbers outside the defined range are always mapped to .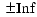

Note    You can use the MATLAB commands realmin and realmax to determine the dynamic range of double-precision floating-point values for your computer.

Precision

Due to a finite word size, a floating-point number is only an approximation of the "true" value. Therefore, it is important to have an understanding of the precision (or accuracy) of a floating-point result. In general, a value v with an accuracy q is specified by 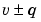. For IEEE floating-point numbers,

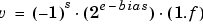and 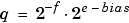. Thus, the precision is associated with the number of bits in the fraction field.

Note    In MATLAB, floating-point relative accuracy is given by the command eps, which returns the distance from 1.0 to the next largest floating-point number. For a computer that supports the IEEE Standard 754, eps = 2-52 or 2.2204 510-16.

Floating-Point Data Type Parameters

The high and low limits, exponent bias, and precision for the supported floating-point data types are given below.

Data Type	Low Limit	High Limit	Exponent Bias	Precision
Single		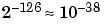	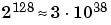127
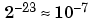Double		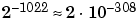	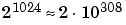1023
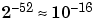Nonstandard

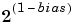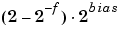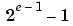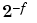Due to the sign/magnitude representation of floating-point numbers, there are two representations of zero, one positive and one negative. For both representations e = 0 and 0.f = 0.0.

The IEEE Format

Exceptional Arithmetic