| Fixed-Point Blockset | |
Exceptional Arithmetic
In addition to specifying a floating-point format, the IEEE Standard 754 specifies practices and procedures so that predictable results are produced independently of the hardware platform. Specifically, denormalized numbers, Inf, and NaN are defined to deal with exceptional arithmetic (underflow and overflow).
If an underflow or overflow is handled as Inf or NaN, then significant processor overhead is required to deal with this exception. Although the IEEE Standard 754 specifies practices and procedures to deal with exceptional arithmetic conditions in a consistent manner, microprocessor manufacturers may handle these conditions in ways that depart from the standard. Some of the alternative approaches, such as saturation and wrapping, are discussed in Arithmetic Operations.
Denormalized Numbers
Denormalized numbers are used to handle cases of exponent underflow. When the exponent of the result is too small (i.e., a negative exponent with too large a magnitude), the result is denormalized by right-shifting the fraction and leaving the exponent at its minimum value. The use of denormalized numbers is also referred to as gradual underflow. Without denormalized numbers, the gap between the smallest representable nonzero number and zero is much wider than the gap between the smallest representable nonzero number and the next larger number. Gradual underflow fills that gap and reduces the impact of exponent underflow to a level comparable with round off among the normalized numbers. Thus, denormalized numbers provide extended range for small numbers at the expense of precision.
Inf
Arithmetic involving Inf (infinity) is treated as the limiting case of real arithmetic, with infinite values defined as those outside the range of representable numbers, or
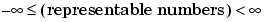. With the exception of the special cases discussed below (NaN), any arithmetic operation involving Inf yields Inf. Inf is represented by the largest biased exponent allowed by the format and a fraction of zero.
NaN
A NaN (not-a-number) is a symbolic entity encoded in floating-point format. There are two types of NaN: signaling and quiet. A signaling NaN signals an invalid operation exception. A quiet NaN propagates through almost every arithmetic operation without signaling an exception. The following operations result in a NaN: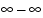 
, 
, 
, 
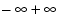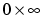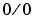, and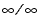 
.
Both types of NaN are represented by the largest biased exponent allowed by the format and a fraction that is nonzero. The bit pattern for a quiet NaN is given by 0.f where the most significant number in f must be a one, while the bit pattern for a signaling NaN is given by 0.f where the most significant number in f must be zero and at least one of the remaining numbers must be nonzero.
| | Range and Precision | Arithmetic Operations | |