Financial Toolbox

Plotting Sensitivities of an Option

This example creates a three-dimensional plot showing how gamma changes relative to price for a Black-Scholes option. Recall that gamma is the second derivative of the option price relative to the underlying security price. The plot shows a three-dimensional surface whose z-value is the gamma of an option as price (x-axis) and time (y-axis) vary. It adds yet a fourth dimension by showing option delta (the first derivative of option price to security price) as the color of the surface. This example M-file is ftgex2.m.

First set the price range of the options, and set the time range to one year divided into half-months and expressed as fractions of a year.

• Range = 10:70;
  Span = length(Range);
  j = 1:0.5:12;
  Newj = j(ones(Span,1),:)'/12;
  

For each time period create a vector of prices from 10 to 70 and create a matrix of all ones.

• JSpan = ones(length(j),1);
  NewRange = Range(JSpan,:);
  Pad = ones(size(Newj));
  

Call the toolbox gamma and delta sensitivity functions. Exercise price is $40, risk-free interest rate is 10%, and volatility is 0.35 for all prices and periods. Gamma is the z-axis, delta is the color.

• ZVal = blsgamma(NewRange, 40*Pad, 0.1*Pad, Newj, 0.35*Pad);
  Color = blsdelta(NewRange, 40*Pad, 0.1*Pad, Newj, 0.35*Pad);
  

Draw the surface as a mesh, add axis labels and a title. The axes range from 10 to 70, 1 to 12, and -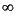 to .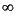

• mesh(Range, j, ZVal, Color);
  xlabel('Stock Price ($)');
  ylabel('Time (months)');
  zlabel('Gamma');
  title('Call Option Sensitivity Measures');
  axis([10 70  1 12  -inf inf]);
  

Finally add a box around the whole plot, annotate the colors with a bar, and label the colorbar.

• set(gca, 'box', 'on');
  colorbar('horiz');
  a = findobj(gcf, 'type', 'axes');
  set(get(a(2), 'xlabel'), 'string', 'Delta');
  
  
  

Producing Graphics with the Toolbox

Plotting Sensitivities of a Portfolio of Options