

| Function Reference |   |
Design continuous- or discrete-time Kalman estimator
Syntax
[kest,L,P] = kalman(sys,Qn,Rn,Nn) [kest,L,P,M,Z] = kalman(sys,Qn,Rn,Nn) % discrete time only [kest,L,P] = kalman(sys,Qn,Rn,Nn,sensors,known)
Description
kalman
designs a Kalman state estimator given a state-space model of the plant and the process and measurement noise covariance data. The Kalman estimator is the optimal solution to the following continuous or discrete estimation problems.
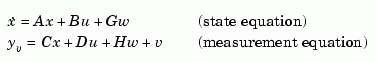
with known inputs 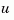 and process and measurement white noise
and process and measurement white noise 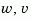 satisfying
satisfying
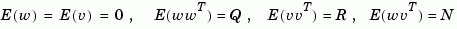
construct a state estimate 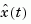 that minimizes the steady-state error covariance
that minimizes the steady-state error covariance
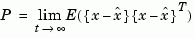
The optimal solution is the Kalman filter with equations
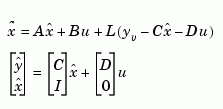
where the filter gain 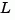 is determined by solving an algebraic Riccati equation. This estimator uses the known inputs
is determined by solving an algebraic Riccati equation. This estimator uses the known inputs 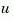 and the measurements
and the measurements 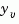 to generate the output and state estimates
to generate the output and state estimates 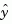 and
and 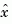 . Note that
. Note that 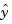 estimates the true plant output
estimates the true plant output
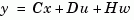
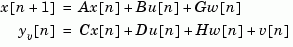
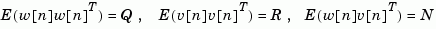
the Kalman estimator has equations
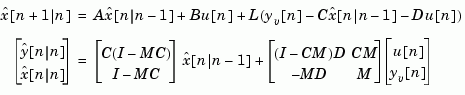
and generates optimal "current" output and state estimates 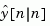 and
and 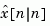 using all available measurements including
using all available measurements including 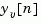 . The gain matrices
. The gain matrices 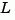 and
and 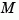 are derived by solving a discrete Riccati equation. The innovation gain
are derived by solving a discrete Riccati equation. The innovation gain 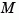 is used to update the prediction
is used to update the prediction 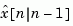 using the new measurement
using the new measurement 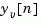 .
.
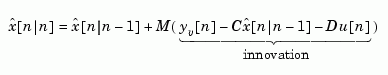
Usage
[kest,L,P] = kalman(sys,Qn,Rn,Nn) returns a state-space model kest of the Kalman estimator given the plant model sys and the noise covariance data Qn, Rn, Nn (matrices 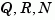 above).
above). sys must be a state-space model with matrices
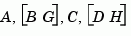
The resulting estimator kest has 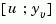 as inputs and
as inputs and 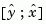 (or their discrete-time counterparts) as outputs. You can omit the last input argument
(or their discrete-time counterparts) as outputs. You can omit the last input argument Nn when 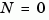 .
.
The function kalman handles both continuous and discrete problems and produces a continuous estimator when sys is continuous, and a discrete estimator otherwise. In continuous time, kalman also returns the Kalman gain L and the steady-state error covariance matrix P. Note that P is the solution of the associated Riccati equation. In discrete time, the syntax
returns the filter gain 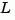 and innovations gain
and innovations gain 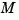 , as well as the steady-state error covariances
, as well as the steady-state error covariances
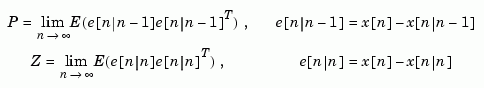
for more general plants sys where the known inputs 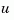 and stochastic inputs
and stochastic inputs 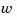 are mixed together, and not all outputs are measured. The index vectors
are mixed together, and not all outputs are measured. The index vectors sensors and known then specify which outputs 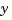 of
of sys are measured and which inputs 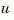 are known. All other inputs are assumed stochastic.
are known. All other inputs are assumed stochastic.
Example
See LQG Design for the x-Axis and Kalman Filtering for examples that use the kalman function.
Limitations
The plant and noise data must satisfy:
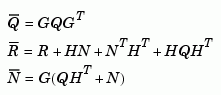
See Also
care
dare
estim
kalmd
lqgreg
lqr
References
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1990.
 | issiso | kalmd |  |