

| Function Reference |   |
Design discrete Kalman estimator for continuous plant
Syntax
Description
kalmd
designs a discrete-time Kalman estimator that has response characteristics similar to a continuous-time estimator designed with kalman. This command is useful to derive a discrete estimator for digital implementation after a satisfactory continuous estimator has been designed.
[kest,L,P,M,Z] = kalmd(sys,Qn,Rn,Ts)
produces a discrete Kalman estimator kest with sample time Ts for the continuous-time plant

with process noise 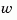 and measurement noise
and measurement noise 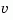 satisfying
satisfying
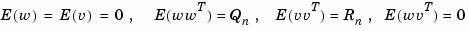
The estimator kest is derived as follows. The continuous plant sys is first discretized using zero-order hold with sample time Ts (see c2d entry), and the continuous noise covariance matrices 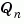 and
and 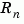 are replaced by their discrete equivalents
are replaced by their discrete equivalents
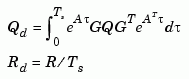
The integral is computed using the matrix exponential formulas in [2]. A discrete-time estimator is then designed for the discretized plant and noise. See kalman for details on discrete-time Kalman estimation.
kalmd also returns the estimator gains L and M, and the discrete error covariance matrices P and Z (see kalman for details).
Limitations
The discretized problem data should satisfy the requirements for kalman.
See Also
kalman
lqgreg
lqrd
References
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1990.
[2] Van Loan, C.F., "Computing Integrals Involving the Matrix Exponential," IEEE Trans. Automatic Control, AC-15, October 1970.
 | kalman | lft |  |