

| System Identification Toolbox |   |
Black-Box, Discrete Time Parametrizations
Suppose first that there is no particular knowledge about the internal structure of the discrete-time state-space model (3-15). Any linear model is sought. A simple approach then is to use
This estimates a state-space model of an order (among 1 to 10) that seems reasonable.
To find a black-box model of a certain order n, use
To get a plot, from which the order can be determined among a list of orders nn = [n1,n2,...,nN], use
All these black-box models are initialized by the subspace method n4sid. To obtain the estimate from this routine, use
Arbitrarily Structured Models in Discrete and Continuous Time
For state-space models of given structure, most of the effort involved relates to defining and manipulating the structure. This is discussed in Structured State-Space Models with Free Parameters: the idss Model and onwards. Once the structure is defined as ms, you can estimate its parameters with
When the systems are multi-output, the following criterion is used for the minimization,
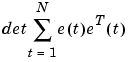
|
(3-42) |
which is the maximum likelihood criterion for Gaussian noise with unknown covariance matrix.
The numerical minimization of the prediction error criterion (3-39) or (3-42) can be a difficult problem for general model parametrizations. The criterion, as a function of the free parameters, can define a complicated surface with many local minima, narrow valleys, and so on. This may require substantial interaction from the user, in providing reasonable initial parameter values, and also by freezing certain parameter values (using the property FixedParameters) while allowing others to be free. Note that pem easily allows the freezing of any parameters to their current/nominal values. The model structure can also be directly manipulated as described in Structured State-Space Models with Free Parameters: the idss Model. A procedure that is often used for state-space models is to allow the noise parameter in the K matrix free only when a reasonable model of the dynamic part has been obtained.
 | General Polynomial Black-Box Models | Optional Variables |  |