

| System Identification Toolbox |   |
Estimating Parametric Models
Given a description (3-10) and having observed the input-output data u, y, the (prediction) errors 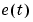 in (3-10) can be computed as
in (3-10) can be computed as
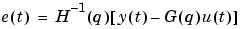
|
(3-36) |
These errors are, for given data y and u, functions of G and H. These in turn are parametrized by the polynomials in (3-14)-(3-19) or by entries in the state-space matrices defined in (3-26)-(3-29). The most common parametric identification method is to determine estimates of G and H by minimizing
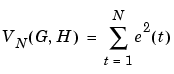
|
(3-37) |
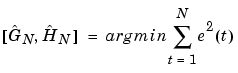
|
(3-38) |
This is called a prediction error method. For Gaussian disturbances it coincides with the maximum likelihood method. (See Chapter 7 in Ljung (1999).)
A somewhat different philosophy can be applied to the ARX model (3-14). By forming filtered versions of the input
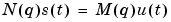
|
(3-39) |
and by multiplying (3-14) with 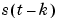 ,
,  , 2,
, 2, , na and
, na and 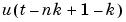 ,
, 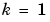 , 2,
, 2,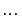 , nb and summing over t, the noise in (3-14) can be correlated out and solved for the dynamics. This gives the instrumental variable method, and
, nb and summing over t, the noise in (3-14) can be correlated out and solved for the dynamics. This gives the instrumental variable method, and 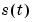 are called the instruments. (See Section 7.6 in Ljung (1999).)
are called the instruments. (See Section 7.6 in Ljung (1999).)
 | Estimating Spectra and Frequency Functions | Subspace Methods for Estimating State-Space Models |  |