System Identification Toolbox

Estimating Spectra and Frequency Functions

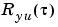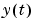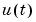This section describes methods that estimate the frequency functions and spectra (3-11) directly. The cross-covariance function between and is defined as 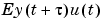analogously to (3-7). Its Fourier transform, the cross spectrum, 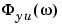is defined analogously to (3-6). Provided that the input 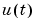is independent of 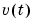, the relationship (3-1) implies the following relationships between the spectra.

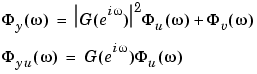
(3-32)

By estimating the various spectra involved, the frequency function and the disturbance spectrum can be estimated as follows.

Form estimates of the covariance functions (as defined in (3-7)) 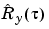, , 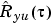and 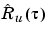, using

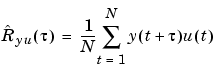
(3-33)

and analog expressions for the others. Then, form estimates of the corresponding spectra

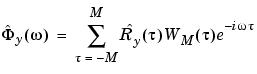
(3-34)

and analogously for 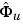and 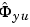. Here 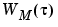is the so-called lag window and M is the width of the lag window. The estimates are then formed as

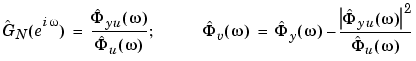
(3-35)

This procedure is known as spectral analysis. (See Chapter 6 in Ljung (1999).)

Estimating Impulse Responses

Estimating Parametric Models