Tutorial (System Identification Toolbox)

System Identification Toolbox

Spectral Analysis

The function spa performs spectral analysis according to the procedure in (3-35)-(3-37).

```
g = spa(Data)
```

Here Data contains the output-input data in the iddata object as above. g is returned as an idfrd (Identified frequency domain) model object, that contains the estimated frequency function 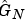and the estimated disturbance spectrum 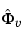in (3-37), as well as estimated uncertainty covariances. The idfrd object is described in the "Command Reference" chapter, but for normal use you do not have to bother about these details. The frequency function, or frequency response, G in g can be graphed by the commands bode, ffplot, or nyquist. The noise spectrum is retrieved by g('n') ('n' for "Noise") so

```
g = spa(Data)
bode(g)
bode(g('n'))
```

performs the spectral analysis, and plots first G and then 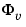. bode gives logarithmic amplitude and frequency scales (in rad/sec) and linear phase scale, while ffplot gives linear frequency scales (in Hz). The uncertainty of the estimates is displayed by adding the argument 'sd' as in

```
bode(g,'sd',3)
```

which will display, by dash-dotted lines, a confidence region around the estimate, that corresponds to (in this case) three standard deviations. Adding an argument 'fill' will show the uncertainty region instead as a filled region.

```
bode(g,'sd',3,'fill')
```

Similarly

```
nyquist(g)
```

gives a Nyquist plot of the frequency function, i.e. a plot of the real part versus the imaginary part of G

If Data = y is a time series, that is Data has no input channel, spa returns an estimate of the spectrum of that signal:

```
g= spa(y)
ffplot(g)
```

In the computations (3-35)-(3-37), spa uses as a lag window the Hamming window for 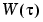with a default length M equal to the minimum of 30 and a tenth of the number of data points. This window size M can be changed to an arbitrary number by

```
g = spa(Data,M)
```

The rule is that as M increases, the estimated frequency functions show sharper details, but are also more affected by random disturbances. A typical sequence of commands that test different window sizes is

g10 = spa(Data,10)
g25 = spa(Data,25)
g50 = spa(Data,50)
bode(g10, g25, g50)

An empirical transfer function estimate is obtained as the ratio of the output and input Fourier transforms with

```
g = etfe(Data)
```

This can also be interpreted as the spectral analysis estimate for a window size that is equal to the data length. For time series, etfe gives the periodogram as a spectral estimate. The function also allows some smoothing of the crude estimate; it can be a good alternative for signals and systems with sharp resonances. See Function Reference for more information.

Correlation Analysis More on the Data Representation in iddata