

| Design Case Studies |   |
Cross-Coupling Between Axes
The 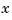 /
/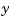 thickness regulation, is a MIMO problem. So far you have treated each axis separately and closed one SISO loop at a time. This design is valid as long as the two axes are fairly decoupled. Unfortunately, this rolling mill process exhibits some degree of cross-coupling between axes. Physically, an increase in hydraulic force along the
thickness regulation, is a MIMO problem. So far you have treated each axis separately and closed one SISO loop at a time. This design is valid as long as the two axes are fairly decoupled. Unfortunately, this rolling mill process exhibits some degree of cross-coupling between axes. Physically, an increase in hydraulic force along the 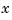 -axis compresses the material, which in turn boosts the repelling force on the
-axis compresses the material, which in turn boosts the repelling force on the 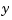 -axis cylinders. The result is an increase in
-axis cylinders. The result is an increase in 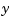 -thickness and an equivalent (relative) decrease in hydraulic force along the
-thickness and an equivalent (relative) decrease in hydraulic force along the 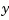 -axis.
-axis.
The figure below shows the coupling.
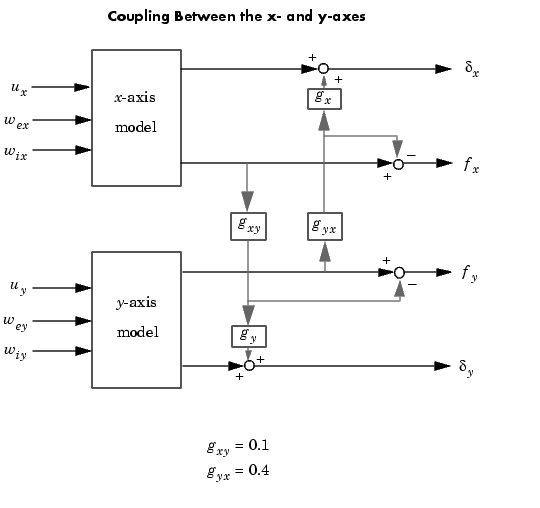
Accordingly, the thickness gaps and rolling forces are related to the outputs 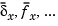 of the
of the 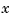 - and
- and 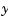 -axis models by
-axis models by
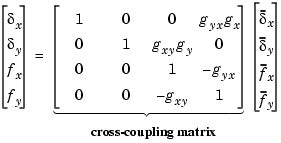
Let's see how the previous "decoupled" LQG design fares when cross-coupling is taken into account. To build the two-axes model, shown in "Coupling Between the x- and y-axes" above, append the models Px and Py for the 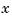 - and
- and 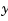 -axes.
-axes.
For convenience, reorder the inputs and outputs so that the commands and thickness gaps appear first.
Finally, place the cross-coupling matrix in series with the outputs.
gxy = 0.1; gyx = 0.4; CCmat = [eye(2) [0 gyx*gx;gxy*gy 0] ; zeros(2) [1 -gyx;-gxy 1]] Pc = CCmat * P Pc.outputname = P.outputname
To simulate the closed-loop response, also form the closed-loop model by
feedin = 1:2 % first two inputs of Pc are the commands feedout = 3:4 % last two outputs of Pc are the measurements cl = feedback(Pc,append(Regx,Regy),feedin,feedout,+1)
You are now ready to simulate the open- and closed-loop responses to the driving white noises wx (for the 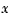 -axis) and
-axis) and wy (for the 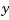 -axis).
-axis).
The response reveals a severe deterioration in regulation performance along the 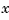 -axis (the peak thickness variation is about four times larger than in the simulation without cross-coupling). Hence, designing for one loop at a time is inadequate for this level of cross-coupling, and you must perform a joint-axis MIMO design to correctly handle coupling effects.
-axis (the peak thickness variation is about four times larger than in the simulation without cross-coupling). Hence, designing for one loop at a time is inadequate for this level of cross-coupling, and you must perform a joint-axis MIMO design to correctly handle coupling effects.
 | LQG Design for the y-Axis | MIMO LQG Design |  |