

| Design Case Studies |   |
MIMO LQG Design
Start with the complete two-axis state-space model Pc derived above. The model inputs and outputs are
Pc.inputname ans = 'u-x' 'u-y' 'w-ex' 'w-ix' 'w_ey' 'w_iy' P.outputname ans = 'x-gap' 'y-gap' 'x-force' 'y-force'
As earlier, add low-pass filters in series with the 'x-gap' and 'y-gap' outputs to penalize only low-frequency thickness variations.
Next, design the LQ gain and state estimator as before (there are now two commands and two measurements).
k = lqry(Pdes(1:2,1:2),eye(2),1e-4*eye(2)) % LQ gain est = kalman(Pdes(3:4,:),eye(4),1e3*eye(2)) % Kalman estimator RegMIMO = lqgreg(est,k) % form MIMO LQG regulator
The resulting LQG regulator RegMIMO has two inputs and two outputs.
Plot its singular value response (principal gains).
Next, plot the open- and closed-loop time responses to the white noise inputs (using the MIMO LQG regulator for feedback).
% Form the closed-loop model cl = feedback(Pc,RegMIMO,1:2,3:4,+1); % Simulate with lsim using same noise inputs lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)
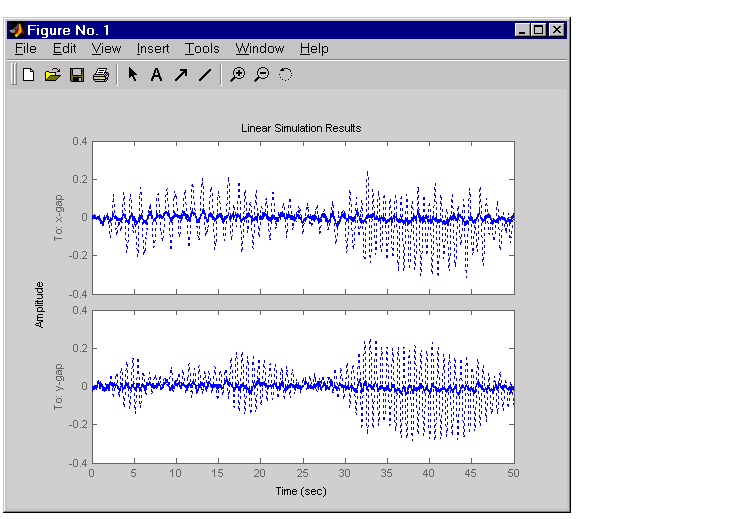
The MIMO design is a clear improvement over the separate SISO designs for each axis. In particular, the level of 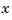 /
/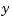 thickness variation is now comparable to that obtained in the decoupled case. This example illustrates the benefits of direct MIMO design for multivariable systems.
thickness variation is now comparable to that obtained in the decoupled case. This example illustrates the benefits of direct MIMO design for multivariable systems.
 | Cross-Coupling Between Axes | Kalman Filtering |  |