

| Wavelet Toolbox |   |
Continuous or Discrete Analysis?
When is continuous analysis more appropriate than discrete analysis? To answer this, consider the related questions: Do you need to know all values of a continuous decomposition to reconstruct the signal s exactly? Can you perform nonredundant analysis?
When the energy of the signal is finite, not all values of a decomposition are needed to exactly reconstruct the original signal, provided that you are using a wavelet that satisfies some admissibility condition (see [Dau92] pages 7, 24, and 27). Usual wavelets satisfy this condition. In which case, a continuous-time signal s is characterized by the knowledge of the discrete transform 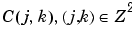 .
.
In such cases, discrete analysis is sufficient and continuous analysis is redundant. When the signal is recorded in continuous time or on a very fine time grid, both analyses are possible. Which should be used? It depends; each one has its own advantages:
Why Are Wavelets Useful for Space-Saving Coding?
The family of functions ( 0,k;
0,k; j,l) j
j,l) j  0,
0, 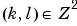 used for the analysis is an orthogonal basis, therefore leading to nonredundancy. The orthogonality properties are
used for the analysis is an orthogonal basis, therefore leading to nonredundancy. The orthogonality properties are 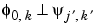 as soon as
as soon as 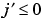 , and
, and 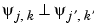 as soon as
as soon as 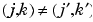 .
.
Let us remember that for a one-dimensional signal, 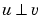 stands for
stands for
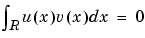
For biorthogonal wavelets, the idea is similar.
What Is the Advantage Having Zero Average and Sometimes Several Vanishing Moments?
When the wavelet's k + 1 moments are equal to zero (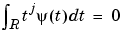 for
for
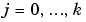 ) all the polynomial signals
) all the polynomial signals
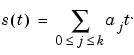 have zero wavelet coefficients.
have zero wavelet coefficients.
As a consequence, the details are also zero. This property ensures the suppression of signals that are polynomials of a degree lower or equal to k.
What About the Regularity of a Wavelet 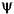 ?
?
In theoretical and practical studies, the notion of regularity has been increasing in importance. Wavelets are tools used to study regularity and to conduct local studies. Deterministic fractal signals or Brownian motion trajectories are locally very irregular; for example, the latter are continuous signals, but their first derivative exists almost nowhere.
The definition of the concept of regularity is somewhat technical. To make things simple, we will define the regularity s of a signal f.
If the signal is s-time continuously differentiable at x0 and s is an integer (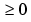 ), then the regularity is s.
), then the regularity is s.
If the derivative of f of order m resembles 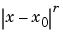 locally around x0, then s = m + r with 0 < r < 1.
locally around x0, then s = m + r with 0 < r < 1.
The regularity of f in a domain is that of its least regular point.
The greater s, the more regular the signal.
The regularity of certain wavelets is known. The following table gives some indications for Daubechies wavelets.
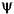 |
db1 = Haar |
db2 |
db3 |
db4 |
db5 |
db7 |
db10 |
| Regularity |
Discontinuous |
0.5 |
0.91 |
1.27 |
1.59 |
2.15 |
2.90 |
We have an asymptotic relation linking the size of the support of the Daubechies wavelets dbN and their regularity: when 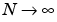 ,
,
length(support) = 2N, regularity 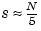 .
.
The functions are more regular at certain points than at others (see Figure 6-9,).
Figure 6-9: Zooming in on db3 Wavelet
Selecting a regularity and a wavelet for the regularity is useful in estimations of the local properties of functions or signals. This can be used, for example, to make sure that a signal has a constant regularity at all points. Work by Donoho, Johnstone, Kerkyacharian, and Picard on function estimation and nonlinear regression is currently under way to adapt the statistical estimators to unknown regularity. See also the remarks by I. Daubechies (see [Dau92] page 301).
From a practical viewpoint, these questions arise in the world of finance in dealing with monetary and stock markets where detailed studies of very fast transactions are required.
Are Wavelets Useful in Fields Other Than Signal or Image Processing?
What Functions Are Candidates to Be a Wavelet?
If a function f is continuous, has null moments, decreases quickly towards 0 when x tends towards infinity, or is null outside a segment of R, it is a likely candidate to become a wavelet.
More precisely, the admissibility condition for 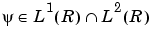 is
is
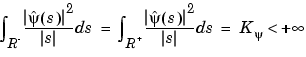
The family of shifts and dilations of 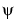 allows all finite energy signals to be reconstructed using the details in all scales. This allows only continuous analysis.
allows all finite energy signals to be reconstructed using the details in all scales. This allows only continuous analysis.
In the toolbox, the 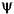 wavelet is usually associated with a scaling function
wavelet is usually associated with a scaling function 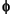 . There are, however, some
. There are, however, some 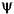 wavelets for which we do not know how to associate a
wavelets for which we do not know how to associate a 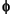 . In some cases we know how to prove that
. In some cases we know how to prove that 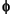 does not exist, for example, the Mexican hat wavelet.
does not exist, for example, the Mexican hat wavelet.
Is It Easy to Build a New Wavelet?
For a minimal requirement on the wavelet properties, it is easy to build a new wavelet, but not very interesting. But if more interesting properties (like the existence of 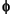 for example) are needed, then building the wavelet is more difficult.
for example) are needed, then building the wavelet is more difficult.
Very few wavelets have an explicit analytical expression. Notable exceptions are wavelets that are piecewise polynomials (Haar, Battle-Lemarié; see [Dau92] page 146), Morlet, or Mexican hat.
Wavelets, even db2, db3, ..., are defined by functional equations. The solution is numerical, and is accomplished using a fairly simple algorithm.
The basic property is the existence of a linear relation between the two functions 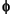 (x/2) and
(x/2) and 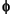 (x). Another relation of the same type links
(x). Another relation of the same type links 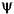 (x/2) to
(x/2) to 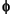 (x). These are the relations of the two scales, the twin-scale relations.
(x). These are the relations of the two scales, the twin-scale relations.
Indeed there are two sequences h and g of coefficients such that
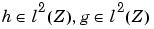
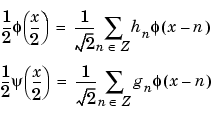
By rewriting these formulas using Fourier transforms (expressed using a hat) we obtain
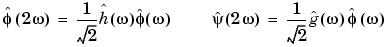
There are 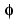 functions for which the h has a finite impulse response (FIR): there is only a finite number of nonzero hn coefficients. The associated wavelets were built by I. Daubechies (see [Dau92] in References) and are used extensively in the toolbox. The reader can refer to page 164 and Chapter 10 of the book Wavelets and Filter Banks, by Strang and Nguyen (see [StrN96] in References).
functions for which the h has a finite impulse response (FIR): there is only a finite number of nonzero hn coefficients. The associated wavelets were built by I. Daubechies (see [Dau92] in References) and are used extensively in the toolbox. The reader can refer to page 164 and Chapter 10 of the book Wavelets and Filter Banks, by Strang and Nguyen (see [StrN96] in References).
What Is the Link Between Wavelet and Fourier Analysis?
Wavelet analysis complements the Fourier analysis for which there are several MATLAB functions: fft, spa, etfe, spectrum, and sptool in the Signal Processing Toolbox.
Fourier analysis uses the basic functions sin(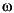 t), cos(
t), cos(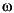 t), and exp(i
t), and exp(i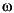 t).
t).
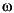 1 t) + 0.5 sin(
1 t) + 0.5 sin(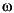 2 t) - cos(
2 t) - cos(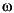 3 t).
3 t).
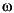 will depend on all values in the signal. To limit the difficulties involved, it is possible to "window" the signal using a regular function, which is zero or nearly zero outside a time segment [-m, m].
will depend on all values in the signal. To limit the difficulties involved, it is possible to "window" the signal using a regular function, which is zero or nearly zero outside a time segment [-m, m].
We then build "a well localized slice" as I. Daubechies calls it (see page 2 of [Dau92] listed in References). The windowed-Fourier analysis coefficients are the doubly indexed coefficients:
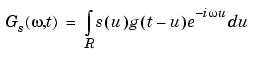
The analogy of this formula with that of the wavelet coefficients is obvious:
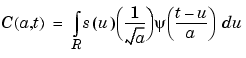
The large values of a correspond to small values of 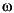 .
.
The Fourier coefficient 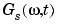 depends on the values of the signal s on the segment [t - m, t + m] with a constant width. If
depends on the values of the signal s on the segment [t - m, t + m] with a constant width. If 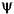 , like g, is zero outside of [-m, m], the C(a,t) coefficients will depend on the values of the signal s on the segment [t - am, t + am] of width 2am, which varies as a function of a. This slight difference solves several difficulties, allowing a kind of time-windowed analysis, different at the various scales a.
, like g, is zero outside of [-m, m], the C(a,t) coefficients will depend on the values of the signal s on the segment [t - am, t + am] of width 2am, which varies as a function of a. This slight difference solves several difficulties, allowing a kind of time-windowed analysis, different at the various scales a.
The wavelets stay competitive, however, even in contexts considered favorable for the Fourier technique. I. Daubechies (see [Dau92] pages 3 to 6) gives an example of windowed-Fourier processing and complex Morlet wavelet processing,
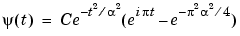 with
with 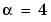 , of a signal composed mainly of the sum of two sines. This wavelet analysis gives good results.
, of a signal composed mainly of the sum of two sines. This wavelet analysis gives good results.
How to Connect Scale to Frequency?
A common question is, what is the relationship between scale and frequency?
The answer can only be given in a broad sense, and it's better to speak about the pseudo-frequency corresponding to a scale.
A way to do it is to compute the center frequency Fc of the wavelet and to use the following relationship (see [Abr97] in References).
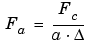
 is the sampling period.
is the sampling period.
The idea is to associate with a given wavelet a purely periodic signal of frequency Fc. The frequency maximizing the fft of the wavelet modulus is Fc. The function centfrq can be used to compute the center frequency and it allows the plotting of the wavelet with the associated approximation based on the center frequency. Figure 6-10, shows some examples generated using the centfrq function.
As you can see, the center frequency-based approximation captures the main wavelet oscillations. So the center frequency is a convenient and simple characterization of the leading dominant frequency of the wavelet.
If we accept to associate the frequency Fc to the wavelet function, then when the wavelet is dilated by a factor a, this center frequency becomes Fc / a. Lastly, if the underlying sampling period is  , it is natural to associate to the scale a the frequency
, it is natural to associate to the scale a the frequency
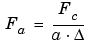
The function scal2frq computes this correspondence.
Figure 6-10: Center Frequencies for Real and Complex Wavelets
To illustrate the behavior of this procedure, consider the following simple test. We generate sine functions of sensible frequencies F0. For each function, we shall try to detect this frequency by a wavelet decomposition followed by a translation of scale to frequency. More precisely, after a discrete wavelet decomposition, we identify the scale a* corresponding to the maximum value of the energy of the coefficients. The translated frequency F* is then given by
The F* values are close to the chosen F0. The plots at the end of the example present the periods instead of the frequencies. If we change the F0 values slightly, the results remain satisfactory.
% Set sampling period and wavelet name. delta = 0.1; wname = 'coif3'; % Set scales. amax = 7; a = 2.^[1:amax]; % Compute associated pseudo-frequencies. f = scal2frq(a,wname,delta); % Compute associated pseudo-periods. per = 1./f; % Plot pseudo-periods versus scales. subplot(211), plot(a,per) title(['Wavelet: ',wname, ', Sampling period: ',num2str(delta)]) xlabel('Scale') ylabel('Computed pseudo-period') % For each scale 2^i: % - generate a sine function of period per(i); % - perform a wavelet decomposition; % - identify the highest energy level; % - compute the detected pseudo-period. for i = 1:amax % Generate sine function of period % per(i) at sampling period delta. t = 0:delta:100; x = sin((t.*2*pi)/per(i)); % Decompose x at level 9. [c,l] = wavedec(x,9,wname); % Estimate standard deviation of detail coefficients. stdc = wnoisest(c,l,[1:amax]); % Compute identified period. [y,jmax] = max(stdc); idper(i) = per(jmax); end % Compare the detected and computed pseudo-periods. subplot(212), plot(per,idper,'o',per,per) title('Detected vs computed pseudo-period') xlabel('Computed pseudo-period') ylabel('Detected pseudo-period')
Figure 6-11: Detected Versus Computed Pseudo-Periods
 | More About SWT | Wavelet Families: Additional Discussion |  |