Statistics Toolbox

Example: Nonlinear Modeling

The Hougen-Watson model (Bates and Watts, [2]) for reaction kinetics is one specific example of this type. The form of the model is

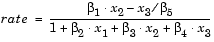
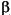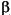where ₁, ₂, ...,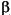₅ are the unknown parameters, and x₁, x₂, and x₃ are the three input variables. The three inputs are hydrogen, n-pentane, and isopentane. It is easy to see that the parameters do not enter the model linearly.

The file reaction.mat contains simulated data from this reaction.

• load reaction
  who
  Your variables are:
  beta        rate        xn          
  model       reactants   yn          
  

The variables are as follows:

• rate is a 13-by-1 vector of observed reaction rates.
• reactants is a 13-by-3 matrix of reactants.
• beta is 5-by-1 vector of initial parameter estimates.
• model is a string containing the nonlinear function name.
• xn is a string matrix of the names of the reactants.
• yn is a string containing the name of the response.

The data and model are explored further in the following sections:

• Fitting the Hougen-Watson Model
• Confidence Intervals on the Parameter Estimates
• Confidence Intervals on the Predicted Responses
• An Interactive GUI for Nonlinear Fitting and Prediction

Fitting the Hougen-Watson Model

The Statistics Toolbox provides the function nlinfit for finding parameter estimates in nonlinear modeling. nlinfit returns the least squares parameter estimates. That is, it finds the parameters that minimize the sum of the squared differences between the observed responses and their fitted values. It uses the Gauss-Newton algorithm with Levenberg-Marquardt modifications for global convergence.

nlinfit requires the input data, the responses, and an initial guess of the unknown parameters. You must also supply the name of a function that takes the input data and the current parameter estimate and returns the predicted responses. In MATLAB terminology, nlinfit is called a "function" function.

Here is the hougen function.

• function yhat = hougen(beta,x)
  %HOUGEN Hougen-Watson model for reaction kinetics.
  %   YHAT = HOUGEN(BETA,X) gives the predicted values of the
  %   reaction rate, YHAT, as a function of the vector of 
  %   parameters, BETA, and the matrix of data, X.
  %   BETA must have five elements and X must have three
  %   columns.
  %
  %   The model form is:
  %   y = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3)
  b1 = beta(1);
  b2 = beta(2);
  b3 = beta(3);
  b4 = beta(4);
  b5 = beta(5);
  x1 = x(:,1);
  x2 = x(:,2);
  x3 = x(:,3);
  yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
  

To fit the reaction data, call the function nlinfit.

• load reaction
  betahat = nlinfit(reactants,rate,'hougen',beta)
  betahat =
      1.2526
      0.0628
      0.0400
      0.1124
      1.1914
  

nlinfit has two optional outputs. They are the residuals and Jacobian matrix at the solution. The residuals are the differences between the observed and fitted responses. The Jacobian matrix is the direct analog of the matrix X in the standard linear regression model.

These outputs are useful for obtaining confidence intervals on the parameter estimates and predicted responses.

Confidence Intervals on the Parameter Estimates

Using nlparci, form 95% confidence intervals on the parameter estimates, betahat, from the reaction kinetics example.

• [betahat,resid,J] = nlinfit(reactants,rate,'hougen',beta);
  betaci = nlparci(betahat,resid,J)
  betaci =
     -0.7467    3.2519
     -0.0377    0.1632
     -0.0312    0.1113
     -0.0609    0.2857
     -0.7381    3.1208
  

Confidence Intervals on the Predicted Responses

Using nlpredci, form 95% confidence intervals on the predicted responses from the reaction kinetics example.

• [yhat,delta] = nlpredci('hougen',reactants,betahat,resid,J);
  opd = [rate yhat delta]
  opd =
      8.5500    8.2937    0.9178
      3.7900    3.8584    0.7244
      4.8200    4.7950    0.8267
      0.0200   -0.0725    0.4775
      2.7500    2.5687    0.4987
     14.3900   14.2227    0.9666
      2.5400    2.4393    0.9247
      4.3500    3.9360    0.7327
     13.0000   12.9440    0.7210
      8.5000    8.2670    0.9459
      0.0500   -0.1437    0.9537
     11.3200   11.3484    0.9228
      3.1300    3.3145    0.8418
  

Matrix opd has the observed rates in column 1 and the predictions in column 2. The 95% confidence interval is column 2±column 3. These are simultaneous confidence intervals for the estimated function at each input value. They are not intervals for new response observations at those inputs, even though most of the confidence intervals do contain the original observations.

Nonlinear Least Squares

An Interactive GUI for Nonlinear Fitting and Prediction