Signal Processing Toolbox

Nonparametric Methods

The following sections discuss the periodogram, modified periodogram, Welch, and multitaper methods of nonparametric estimation, along with the related CSD function, transfer function estimate, and coherence function.

Periodogram

One way of estimating the power spectrum of a process is to simply find the discrete-time Fourier transform of the samples of the process (usually done on a grid with an FFT) and take the magnitude squared of the result. This estimate is called the periodogram.

The periodogram estimate of the PSD of a length-L signal x_L[n] is

where

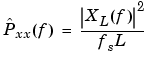
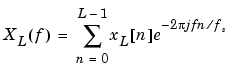
The actual computation of X_L(f) can be performed only at a finite number of frequency points, N, and usually employs the FFT. In practice, most implementations of the periodogram method compute the N-point PSD estimate

where

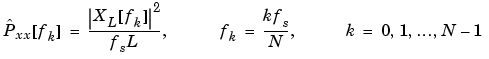
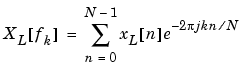
It is wise to choose N > L so that N is the next power of two larger than L. To evaluate X_L[f_k], we simply pad x_L[n] with zeros to length N. If L > N, we must wrap x_L[n] modulo-N prior to computing X_L[f_k].

As an example, consider the following 1001-element signal xn, which consists of two sinusoids plus noise:

• randn('state',0);
  fs = 1000;           % Sampling frequency
  t = (0:fs)/fs;       % One second worth of samples
  A = [1 2];           % Sinusoid amplitudes (row vector)
  f = [150;140];       % Sinusoid frequencies (column vector)
  xn = A*sin(2*pi*f*t) + 0.1*randn(size(t));
  

Note    The three last lines illustrate a convenient and general way to express the sum of sinusoids. Together they are equivalent to    xn = sin(2*pi*150*t) + 2*sin(2*pi*140*t) + 0.1*randn(size(t));

The periodogram estimate of the PSD can be computed by

• Pxx = periodogram(xn,[],'twosided',1024,fs);
  

and a plot of the estimate can be displayed by simply omitting the output argument, as below:

• periodogram(xn,[],'twosided',1024,fs);
  
  
  

The average power can be computed by approximating the integral with the following sum:

• Pow = (fs/length(Pxx)) * sum(Pxx)
  Pow =
      2.5028
  

You can also compute the average power from the one-sided PSD estimate:

• Pxxo = periodogram(xn,[],1024,fs);
  Pow = (fs/(2*length(Pxxo))) * sum(Pxxo)
  Pow =
      2.4979
  

Spectral Estimation Method

Performance of the Periodogram