pmtm (Signal Processing Toolbox)

Estimate the power spectral density using the multitaper method (MTM)

Syntax

[Pxx,w] = pmtm(x,nw)
[Pxx,w] = pmtm(x,nw,nfft)
[Pxx,f] = pmtm(x,nw,nfft,fs)
[Pxx,Pxxc,f] = pmtm(x,nw,nfft,fs)
[Pxx,Pxxc,f] = pmtm(x,nw,nfft,fs,p)
[Pxx,Pxxc,f] = pmtm(x,e,v,nfft,fs,p)
[Pxx,Pxxc,f] = pmtm(x,dpss_params,nfft,fs,p)
[...] = pmtm(...,'method')
[...] = pmtm(...,'range')
pmtm(...)

Description

pmtm estimates the power spectral density (PSD) of the time series x using the multitaper method (MTM) described in [1]. This method uses linear or nonlinear combinations of modified periodograms to estimate the PSD. These periodograms are computed using a sequence of orthogonal tapers (windows in the frequency domain) specified from the discrete prolate spheroidal sequences (see dpss).

[Pxx,w] = pmtm(x,nw) estimates the PSD Pxx for the input signal x, using 2*nw-1 discrete prolate spheroidal sequences as data tapers for the multitaper estimation method. nw is the time-bandwidth product for the discrete prolate spheroidal sequences. If you specify nw as the empty vector [], a default value of 4 is used. Other typical choices are 2, 5/2, 3, or 7/2. pmtm also returns w, a vector of frequencies at which the PSD is estimated. Pxx and w have the same length. The units for frequency are rad/sample.

The power spectral density is calculated in units of power per radians per sample. Real-valued inputs produce (by default) full power one-sided (in frequency) PSDs, while complex-valued inputs produce two-sided PSDs.

In general, the length N of the FFT and the values of the input x determine the length of Pxx and the range of the corresponding normalized frequencies. For this syntax, the (default) length N of the FFT is the larger of 256 and the next power of two greater than the length of the segment. The following table indicates the length of Pxx and the range of the corresponding normalized frequencies for this syntax.

PSD Vector Characteristics for an FFT Length of N (Default)
Real/Complex Input Data
Length of Pxx
Range of the Corresponding Normalized Frequencies

Real-valued
(N/2) +1
[0, ]

Complex-valued
N
[0, 2)

**PSD Vector Characteristics for an FFT Length of N (Default)**
Real/Complex Input Data	Length of Pxx	Range of the Corresponding Normalized Frequencies
Real-valued	(N/2) +1	[0, ]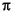
Complex-valued	N	[0, 2)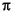

[Pxx,w] = pmtm(x,nw,nfft) uses the multitaper method to estimate the PSD while specifying the length of the FFT with the integer nfft. If you specify nfft as the empty vector [], it adopts the default value for N described in the previous syntax.

The length of Pxx and the frequency range for w depend on nfft and the values of the input x. The following table indicates the length of Pxx and the frequency range for w for this syntax.

PSD and Frequency Vector Characteristics
Real/Complex Input Data
nfft Even/Odd
Length of Pxx
Range of w

Real-valued
Even
(nfft/2 + 1)
[0, ]

Real-valued
Odd
(nfft + 1)/2
[0, )

Complex-valued
Even or odd
nfft
[0, 2)

**PSD and Frequency Vector Characteristics**
Real/Complex Input Data	nfft Even/Odd	Length of Pxx	Range of w
Real-valued	Even	(`nfft`/2 + 1)	[0, ]
Real-valued	Odd	(`nfft` + 1)/2	[0, )
Complex-valued	Even or odd	`nfft`	[0, 2)

[Pxx,f] = pmtm(x,nw,nfft,fs) uses the sampling frequency fs specified as an integer in hertz (Hz) to compute the PSD vector (Pxx) and the corresponding vector of frequencies (f). In this case, the units for the frequency vector f are in Hz. The spectral density produced is calculated in units of power per Hz. If you specify fs as the empty vector [], the sampling frequency defaults to 1 Hz.

The frequency range for f depends on nfft, fs, and the values of the input x. The length of Pxx is the same as in the Table , PSD and Frequency Vector Characteristics above. The following table indicates the frequency range for f for this syntax.

PSD and Frequency Vector Characteristics with fs Specified
Real/Complex Input Data
nfft Even/Odd
Range of f

Real-valued
Even
[0, fs/2]

Real-valued
Odd
[0, fs/2)

Complex-valued
Even or odd
[0, fs)

**PSD and Frequency Vector Characteristics with fs Specified**
Real/Complex Input Data	nfft Even/Odd	Range of f
Real-valued	Even	`[0`, `fs/2`]
Real-valued	Odd	`[0`, `fs/2)`
Complex-valued	Even or odd	[0, `fs`)

[Pxx,Pxxc,f] = pmtm(x,nw,nfft,fs) returns Pxxc, the 95% confidence interval for Pxx. Confidence intervals are computed using a chi-squared approach. Pxxc is a two-column matrix with the same number of rows as Pxx. Pxxc(:,1) is the lower bound of the confidence interval and Pxxc(:,2) is the upper bound of the confidence interval.

[Pxx,Pxxc,f] = pmtm(x,nw,nfft,fs,p) returns Pxxc, the p*100% confidence interval for Pxx, where p is a scalar between 0 and 1. If you don't specify p, or if you specify p as the empty vector [], the default 95% confidence interval is used.

[Pxx,Pxxc,f] = pmtm(x,e,v,nfft,fs,p) returns the PSD estimate Pxx, the confidence interval Pxxc, and the frequency vector f from the data tapers contained in the columns of the matrix e, and their concentrations in the vector v. The length of v is the same as the number of columns in e. You can obtain the data to supply as these arguments from the outputs of dpss.

[Pxx,Pxxc,f] = pmtm(x,dpss_params,nfft,fs,p) uses the cell array dpss_params containing the input arguments to dpss (listed in order, but excluding the first argument) to compute the data tapers. For example, pmtm(x,{3.5,'trace'},512,1000) calculates the prolate spheroidal sequences for nw = 3.5, using nfft = 512, and fs = 1000, and displays the method that dpss uses for this calculation. See dpss for other options.

[...] = pmtm(...,'method') specifies the algorithm used for combining the individual spectral estimates. The string 'method' can be one of the following:

'adapt': Thomson's adaptive nonlinear combination (default)
'unity': A linear combination of the weighted periodograms with unity weights
'eigen': A linear combination of the weighted periodograms with eigenvalue weights

[...] = pmtm(...,'range') specifies the range of frequency values to include in f or w. This syntax is useful when x is real. 'range' can be either:

'twosided': Compute the two-sided PSD over the frequency range [0,fs). This is the default for determining the frequency range for complex-valued x.

If you specify fs as the empty vector, [], the frequency range is [0,1).
If you don't specify fs, the frequency range is [0, 2).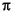

'onesided': Compute the one-sided PSD over the frequency ranges specified for real x. This is the default for determining the frequency range for real-valued x.

Note You can put the string arguments 'range' or 'method' anywhere after the input argument nw or v.

pmtm(...) with no output arguments plots the PSD estimate and the confidence intervals in the current figure window. If you don't specify fs, the 95% confidence interval is plotted. If you do specify fs, the confidence intervals plotted depend on the value of p.

Examples

This example analyzes a sinusoid in white noise:

randn('state',0);
fs = 1000; t = 0:1/fs:0.3;
x = cos(2*pi*t*200) + 0.1*randn(size(t));
[Pxx,Pxxc,f] = pmtm(x,3.5,512,fs,0.99);
psdplot([Pxx Pxxc],f,'hz','db')
title('PMTM PSD Estimate with 99% Confidence Intervals')

See Also

dpss, pburg, pcov, peig, periodogram, pmcov, pmusic, pwelch, psdplot, pyulear

References

[1] Percival, D.B., and A.T. Walden, Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques, Cambridge University Press, 1993.

[2] Thomson, D.J., "Spectrum estimation and harmonic analysis," Proceedings of the IEEE, Vol. 70 (1982), pp. 1055-1096.

pmcov pmusic