Optimization Toolbox

Constrained Example with Bounds

The variables in x can be restricted to certain limits by specifying simple bound constraints to the constrained optimizer function. For fmincon, the command

• x = fmincon(@objfun,x0,[],[],[],[],lb,ub,@confun,options);
  

limits x to be within the range lb <= x <= ub.

To restrict x in Eq. 2-2 to be greater than zero (i.e., 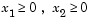), use the commands

• x0 = [-1,1];       % Make a starting guess at the solution
  lb = [0,0];        % Set lower bounds
  ub = [ ];          % No upper bounds
  options = optimset('LargeScale','off');
  [x,fval = ... 
        fmincon(@objfun,x0,[],[],[],[],lb,ub,@confun,options)
  [c, ceq] = confun(x)
  

Note that to pass in the lower bounds as the seventh argument to fmincon, you must specify values for the third through sixth arguments. In this example, we specified [] for these arguments since there are no linear inequalities or linear equalities.

After 13 function evaluations, the solution produced is

• x = 
         0   1.5000
  fval =
         8.5000
  c =
       0
     -10
  ceq =
       []
  

When lb or ub contains fewer elements than x, only the first corresponding elements in x are bounded. Alternatively, if only some of the variables are bounded, then use -inf in lb for unbounded below variables and inf in ub for unbounded above variables. For example,

• lb = [-inf 0];
  ub = [10 inf];
  

bounds 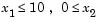( 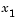has no lower bound and 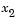has no upper bound). Using inf and -inf give better numerical results than using a very large positive number or a very large negative number to imply lack of bounds.

Note that the number of function evaluations to find the solution is reduced because we further restricted the search space. Fewer function evaluations are usually taken when a problem has more constraints and bound limitations because the optimization makes better decisions regarding step size and regions of feasibility than in the unconstrained case. It is, therefore, good practice to bound and constrain problems, where possible, to promote fast convergence to a solution.

Nonlinear Inequality Constrained Example

Constrained Example with Gradients