Tutorial (System Identification Toolbox)

System Identification Toolbox

Black-Box State-Space Models: the idss Model

The basic state-space models are the following ones: (See also State-Space Models.).

Discrete-Time Innovations Form

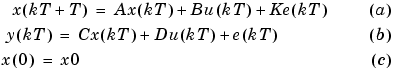
(3-51)

Here T is the sampling interval,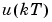 is the input at time instant 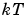, and 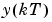is the output at time 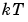. (See Ljung (1999) page 99.)

System Dynamics Expressed in Continuous Time

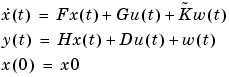
(3-52)

(See Ljung (1999), page 93.) It is often easier to define a parameterized state-space model in continuous time because physical laws are most often described in terms of differential equations. The matrices F, G, H, and D contain elements with physical significance (for example, material constants). The numerical values of these may or may not be known. To estimate unknown parameters based on sampled data (assuming T is the sampling interval) first transform (3-52) to (3-51) using the formulas (3-27). The value of the Kalman gain matrix K in (3-51) or 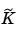in (3-52) depends on the assumed character of the additive noises 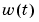and 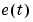in (3-25), and its continuous-time counterpart. Disregard that link and view K in (3-51) (or 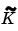in (3-52)) as the basic tool to model the disturbance properties. This gives the directly parametrized innovations form. (See Ljung (1999) page 99.) If the internal noise structure is important, you could use user-defined greybox structures (the idgrey object) as in the example.

The discrete time model (3-51) can be put into the idss model by

```
m = idss(A,B,C,D,K,X0,'Ts',T)
```

and for the continuous-time model (3-52) use

```
m = idss(F,G,H,D,Kt,X0,'Ts',0)
```

Setting the sampling interval Ts to zero means a continuous-time model. The model m can now be used for simulation and it can be examined by the various commands. The parameterization of the matrices is by default "free" that is, any elements in the matrices are freely adjustable by the estimation routines. The parameters will be adjusted to data by

```
me = pem(Data,m)
```

The iterative search for the best fit is then initialized in the nominal matrices A, B, C, D, K, X0. Note that the command me = pem(Data,4), which just defines the model order, first estimates (using n4sid) a starting model m, from which the search is initialized.

In this free parameterization, you can decide how to deal with the disturbance model matrix K. Letting

```
m.DisturbanceModel = 'None'
```

(rather than 'Estimate') fixes the K-matrix to zero, thereby creating an Output-Error model.

Letting

```
m.InitialState ='zero'
```

(rather than 'Estimate') sets the initial state vector x0 to zero.

The property nk determines the delays from the different inputs just as for idpoly models. Thus

```
m.nk = [0,0,...,0]
```

(no delays) means that all elements of the D-matrix should be estimated, while

```
m.nk = [1,1,..,1]
```

fixes the D-matrix to zero.

With the parameterization of A, B, and C being completely free, a basis for the state-space realization is automatically selected to give well-conditioned calculations. An alternative is to specify an observer canonical form for A, B, C by

```
m.sspar = 'Canonical'
```

(rather than 'Free'). This is still a black-box model, since the canonical form covers all models of a certain order. The structure modifications can all be combined at the estimation call

me = pem(Data,m,'sspar','can','dist','none','ini','z')

which is the same as

set(m,'sspar','can','dist','none','ini','z')
me = pem(Data,m);

Multivariable ARX Models: The idarx Model Structured State-Space Models with Free Parameters: the idss Model