

| Function Reference |   |
Design discrete LQ regulator for continuous plant
Syntax
Description
lqrd
designs a discrete full-state-feedback regulator that has response characteristics similar to a continuous state-feedback regulator designed using lqr. This command is useful to design a gain matrix for digital implementation after a satisfactory continuous state-feedback gain has been designed.
[Kd,S,e] = lqrd(A,B,Q,R,Ts)
calculates the discrete state-feedback law
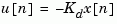
that minimizes a discrete cost function equivalent to the continuous cost function
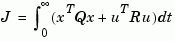
The matrices A and B specify the continuous plant dynamics
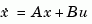
and Ts specifies the sample time of the discrete regulator. Also returned are the solution S of the discrete Riccati equation for the discretized problem and the discrete closed-loop eigenvalues e = eig(Ad-Bd*Kd).
[Kd,S,e] = lqrd(A,B,Q,R,N,Ts)
solves the more general problem with a cross-coupling term in the cost function.
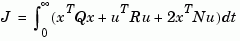
Algorithm
The equivalent discrete gain matrix Kd is determined by discretizing the continuous plant and weighting matrices using the sample time Ts and the zero-order hold approximation.
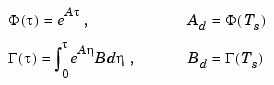
the discretized plant has equations
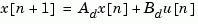
and the weighting matrices for the equivalent discrete cost function are
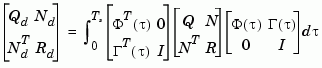
The integrals are computed using matrix exponential formulas due to Van Loan (see [2]). The plant is discretized using c2d and the gain matrix is computed from the discretized data using dlqr.
Limitations
The discretized problem data should meet the requirements for dlqr.
See Also
c2d
dlqr
kalmd
lqr
References
[1] Franklin, G.F., J.D. Powell, and M.L. Workman, Digital Control of Dynamic Systems, Second Edition, Addison-Wesley, 1980, pp. 439-440
[2] Van Loan, C.F., "Computing Integrals Involving the Matrix Exponential," IEEE Trans. Automatic Control, AC-15, October 1970.
 | lqr | lqry |  |