

| Creating and Manipulating Models |   |
Zero-Pole-Gain Models
This section explains how to specify continuous-time SISO and MIMO zero-pole-gain models. The specification for discrete-time zero-pole-gain models is a simple extension of the continuous-time case. See Discrete-Time Models.
SISO Zero-Pole-Gain Models
Continuous-time SISO zero-pole-gain models are of the form
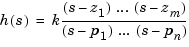
where 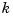 is a real-valued scalar (the gain), and
is a real-valued scalar (the gain), and 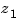 ,...,
,...,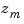 and
and 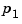 ,...,
,...,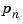 are the real or complex conjugate pairs of zeros and poles of the transfer function
are the real or complex conjugate pairs of zeros and poles of the transfer function 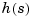 . This model is closely related to the transfer function representation: the zeros are simply the numerator roots, and the poles, the denominator roots.
. This model is closely related to the transfer function representation: the zeros are simply the numerator roots, and the poles, the denominator roots.
There are two ways to specify SISO zero-pole-gain models:
zpk command
The syntax to specify ZPK models directly using zpk is
where z and p are the vectors of zeros and poles, and k is the gain. This produces a ZPK object h that encapsulates the z, p, and k data. For example, typing
You can also specify zero-pole-gain models as rational expressions in the Laplace variable s by:
s as a ZPK model
s.
For example, once s is defined with zpk,
Note
You need only define the ZPK variable s once. All subsequent rational
expressions of s will be ZPK models, unless you convert the variable s to TF.
See Model Conversion for more information on conversion to
other model types.
|
MIMO Zero-Pole-Gain Models
Just as with TF models, you can also specify a MIMO ZPK model by concatenation of its SISO entries (see Model Interconnection Functions).
You can also use the command zpk to specify MIMO ZPK models. The syntax to create a p-by-m MIMO zero-pole-gain model using zpk is
Z is the p-by-m cell array of zeros (Z{i,j} = zeros of 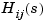 )
)
P is the p-by-m cell array of poles (P{i,j} = poles of 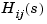 )
)
K is the p-by-m matrix of gains (K(i,j) = gain of 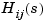 )
)
creates the two-input/two-output zero-pole-gain model
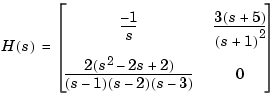
Notice that you use [] as a place-holder in Z (or P) when the corresponding entry of 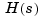 has no zeros (or poles).
has no zeros (or poles).
 | Transfer Function Models | State-Space Models |  |