Getting Started

Pole Placement

The closed-loop pole locations have a direct impact on time response characteristics such as rise time, settling time, and transient oscillations. Root locus uses compensator gains to move closed-loop poles to achieve design specifications for SISO systems. You can, however, use state-space techniques to assign closed-loop poles. This design technique is known as pole placement, which differs from root locus in the following ways:

• Using pole placement techniques, you can design dynamic compensators.
• Pole placement techniques are applicable to MIMO systems.

Pole placement requires a state-space model of the system (use ss to convert other model formats to state space). In continuous time, such models are of the form

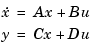
where 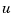is the vector of control inputs, 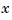is the state vector, and 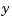is the vector of measurements.

State-Feedback Gain Selection

Under state feedback 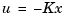, the closed-loop dynamics are given by

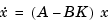
and the closed-loop poles are the eigenvalues of 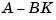. Using the place command, you can compute a gain matrix 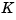that assigns these poles to any desired locations in the complex plane (provided that 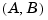is controllable).

For example, for state matrices A and B, and vector p that contains the desired locations of the closed loop poles,

• K = place(A,B,p);
  

computes an appropriate gain matrix K.

State Estimator Design

You cannot implement the state-feedback law 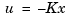unless the full state 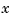is measured. However, you can construct a state estimate 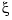such that the law 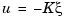retains similar pole assignment and closed-loop properties. You can achieve this by designing a state estimator (or observer) of the form

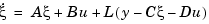
The estimator poles are the eigenvalues of 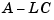, which can be arbitrarily assigned by proper selection of the estimator gain matrix 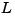, provided that
(C, A) is observable. Generally, the estimator dynamics should be faster than the controller dynamics (eigenvalues of ).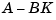

Use the place command to calculate the L matrix

• L = place(A',C',q)
  

where A and C are the state and output matrices, and q is the vector containing the desired closed-loop poles for the observer.

Replacing 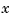by its estimate 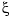in 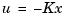yields the dynamic output-feedback compensator

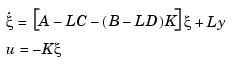
Note that the resulting closed-loop dynamics are

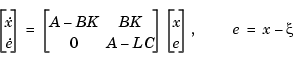
Hence, you actually assign all closed-loop poles by independently placing the eigenvalues of 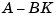and .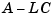

Example.   Given a continuous-time state-space model

• sys_pp = ss(A,B,C,D) 
  

with seven outputs and four inputs, suppose you have designed

• A state-feedback controller gain K using inputs 1, 2, and 4 of the plant as control inputs
• A state estimator with gain L using outputs 4, 7, and 1 of the plant as sensors
• Input 3 of the plant as an additional known input

You can then connect the controller and estimator and form the dynamic compensator using this code.

• controls = [1,2,4];
  sensors = [4,7,1];
  known = [3];
  regulator = reg(sys_pp,K,L,sensors,known,controls)
  

Pole Placement Tools

The Control System Toolbox contains functions to

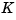• Compute gain matrices and 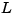that achieve the desired closed-loop pole locations.
• Form the state estimator and dynamic compensator using these gains.

The following table summarizes the commands for pole placement.

Command	Description
acker	SISO pole placement
estim	Form state estimator given estimator gain
place	MIMO pole placement
reg	Form output-feedback compensator given state-feedback and estimator gains

The function acker is limited to SISO systems and should only be used for systems with a small number of states. The function place is a more general and numerically robust alternative to acker.

Caution.   Pole placement can be badly conditioned if you choose unrealistic pole locations. In particular, you should avoid

• Placing multiple poles at the same location.
• Moving poles that are weakly controllable or observable. This typically requires high gain, which in turn makes the entire closed-loop eigenstructure very sensitive to perturbations.

Root Locus Design

Linear-Quadratic-Gaussian (LQG) Design