

| Wavelet Toolbox |   |
De-noising or compression using wavelets
Syntax
[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('gbl',X,'wname',N,THR,SORH,KEEPAPP) [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SORH) [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH)
Description
wdencmp is a one- or two-dimensional de-noising and compression-oriented function.
wdencmp performs a de-noising or compression process of a signal or an image, using wavelets.
[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('gbl',X,'wname',N,THR,SORH, KEEPAPP) returns a de-noised or compressed version XC of input signal X (one- or two-dimensional) obtained by wavelet coefficients thresholding using global positive threshold THR.
Additional output arguments [CXC,LXC] are the wavelet decomposition structure of XC (see wavedec or wavedec2 for more information). PERF0 and PERFL2 are L2-norm recovery and compression score in percentage.
PERFL2 = 100 * (vector-norm of CXC / vector-norm of C)2 if [C,L] denotes the wavelet decomposition structure of X.
If X is a one-dimensional signal and 'wname' an orthogonal wavelet, PERFL2 is reduced to
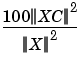
Wavelet decomposition is performed at level N and 'wname' is a string containing wavelet name (see wmaxlev and wfilters for more information). SORH ('s' or 'h') is for soft or hard thresholding (see wthresh for more information). If KEEPAPP = 1, approximation coefficients cannot be thresholded, otherwise it is possible.
wdencmp('gbl',C,L,'wname',N,THR,SORH,KEEPAPP) has the same output arguments, using the same options as above, but obtained directly from the input wavelet decomposition structure [C,L] of the signal to be de-noised or compressed, at level N and using 'wname' wavelet.
For the one-dimensional case and 'lvd' option, [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SORH)or [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH)
have the same output arguments, using the same options as above, but allowing level-dependent thresholds contained in vector THR (THR must be of length N). In addition, the approximation is kept. Note that, with respect to wden (automatic de-noising), wdencmp allows more flexibility and you can implement your own de-noising strategy.
For the two-dimensional case and 'lvd' option,[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SORH) or [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH)
THR must be a matrix 3 by N containing the level-dependent thresholds in the three orientations; horizontal, diagonal, and vertical.
Ideas for de-noising can be found in Chapter 2, "Using Wavelets," and in the "Description" section of the wden function.
The compression features of a given wavelet basis are primarily linked to the relative scarceness of the wavelet domain representation for the signal. The notion behind compression is based on the concept that the regular signal component can be accurately approximated using a small number of approximation coefficients (at a suitably selected level) and some of the detail coefficients.
Like de-noising, the compression procedure contains three steps:
N, a threshold is selected and hard thresholding is applied to the detail coefficients.
The difference with the de-noising procedure is found in step 2.
Examples
% The current extension mode is zero-padding (seedwtmode). % Load original image. load sinsin % X contains the loaded image. % Generate noisy image. init=2055615866; randn('seed',init); x = X + 18*randn(size(X)); % Use wdencmp for image de-noising. % find default values (seeddencmp). [thr,sorh,keepapp] = ddencmp('den','wv',x); % de-noise image using global thresholding option. xd = wdencmp('gbl',x,'sym4',2,thr,sorh,keepapp); % Using some plotting commands, % the following figure is generated.% Load electrical signal and select a part. load leleccum; indx = 2600:3100; x = leleccum(indx); % Use wdencmp for signal compression. % Compress using a fixed threshold. thr=35; [xd,cxd,lxd,perf0,perfl2] = ... wdencmp('gbl',x,'db3',3,thr,'h',1); % Using some plotting commands, % the following figure is generated. % Use wdencmp for signal de-noising. % Find default values (see
ddencmp). [thr,sorh,keepapp] = ddencmp('den','wv',x); % De-noise signal using global thresholding option. xd = wdencmp('gbl',x,'db3',2,thr,sorh,keepapp); % Using some plotting commands, % the following figure is generated. % Load original image. load woman; % X contains the loaded image. x=X(100:200,100:200); nbc = size(map,1); % Use wdencmp for image compression. % Wavelet decomposition of x. n = 5; w = 'sym2'; [c,l] = wavedec2(x,n,w); % Wavelet coefficients thresholding. thr=20; [xd,cxd,lxd,perf0,perfl2] = ... wdencmp('gbl',c,l,w,n,thr,'h',1); % Using some plotting commands, % the following figure is generated. % In addition the first option allows level and orientation- % dependent thresholds. In this case the approximation is kept. % The level-dependent thresholds in the three orientations % horizontal, diagonal and vertical are as follows: thr_h = [17 18]; % Horizontal thresholds. thr_d = [19 20]; % Diagonal thresholds. thr_v = [21 22]; % Vertical thresholds. thr = [thr_h ; thr_d ; thr_v] thr = 17 18 19 20 21 22 [xd,cxd,lxd,perf0,perfl2] = ... wdencmp('lvd',x,'sym8',2,thr,'h');
See Also
ddencmp, wavedec, wavedec2, wdcbm, wdcbm2, wden, wbmpen, wpdencmp, wthresh
References
DeVore, R.A.; B. Jawerth, B.J. Lucier (1992), "Image compression through wavelet transform coding," IEEE Trans. on Inf. Theory, vol. 38, No 2, pp. 719-746.
Donoho, D.L. (1993), "Progress in wavelet analysis and WVD: a ten minute tour," in Progress in wavelet analysis and applications, Y. Meyer, S. Roques, pp. 109-128. Frontières Ed.
Donoho, D.L.; I.M. Johnstone(1994), "Ideal spatial adaptation by wavelet shrinkage," Biometrika, vol 81, pp. 425-455.
Donoho, D.L.; I.M. Johnstone, G. Kerkyacharian, D. Picard (1995), "Wavelet shrinkage: asymptopia," Jour. Roy. Stat. Soc., series B, vol. 57 no. 2, pp. 301-369.
Donoho, D.L.; I.M. Johnstone, "Ideal de-noising in an orthonormal basis chosen from a library of bases," C.R.A.S. Paris, t. 319, Ser. I, pp. 1317-1322.
Donoho, D.L. (1995), "De-noising by soft-thresholding," IEEE Trans. on Inf. Theory, 41, 3, pp. 613-627.
 | wden | wenergy |  |