Statistics Toolbox

Noncentral t Distribution

The following sections provide an overview of the noncentral t distribution.

Background of the Noncentral t Distribution

The noncentral t distribution is a generalization of the familiar Student's t distribution.

If x and s are the mean and standard deviation of an independent random sample of size n from a normal distribution with mean µ and 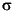² = n, then

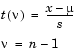
Suppose that the mean of the normal distribution is not µ. Then the ratio has the noncentral t distribution. The noncentrality parameter is the difference between the sample mean and µ.

The noncentral t distribution allows us to determine the probability that we would detect a difference between x and µ in a t test. This probability is the power of the test. As x-µ increases, the power of a test also increases.

Definition of the Noncentral t Distribution

The most general representation of the noncentral t distribution is quite complicated. Johnson and Kotz (1970) give a formula for the probability that a noncentral t variate falls in the range [-t, t].

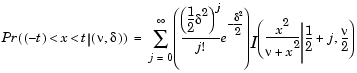
I(x|a,b) is the incomplete beta function with parameters a and b, 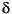 is the noncentrality parameter, and  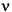is the degrees of freedom.

Example and Plot of the Noncentral t Distribution

The following commands generate a plot of the noncentral t pdf.

• x = (-5:0.1:5)';
  p1 = nctcdf(x,10,1);
  p = tcdf(x,10);
  plot(x,p,'--',x,p1,'-')
  
  
  

Uniform (Continuous) Distribution

The following sections provide an overview of the uniform distribution.

Background of the Uniform Distribution

The uniform distribution (also called rectangular) has a constant pdf between its two parameters a (the minimum) and b (the maximum). The standard uniform distribution (a = 0 and b = 1) is a special case of the beta distribution, obtained by setting both of its parameters to 1.

The uniform distribution is appropriate for representing the distribution of round-off errors in values tabulated to a particular number of decimal places.

Definition of the Uniform Distribution

The uniform cdf is

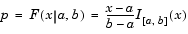
Parameter Estimation for the Uniform Distribution

The sample minimum and maximum are the MLEs of a and b respectively.

Example and Plot of the Uniform Distribution

The example illustrates the inversion method for generating normal random numbers using rand and norminv. Note that the MATLAB function, randn, does not use inversion since it is not efficient for this case.

• u = rand(1000,1);
  x = norminv(u,0,1);
  hist(x)
  
  
  

Student's t Distribution

Weibull Distribution