Statistics Toolbox

Binomial Distribution

The following sections provide an overview of the binomial distribution.

Background of the Binomial Distribution

The binomial distribution models the total number of successes in repeated trials from an infinite population under the following conditions:

• Only two outcomes are possible on each of n trials.
• The probability of success for each trial is constant.
• All trials are independent of each other.

James Bernoulli derived the binomial distribution in 1713 (Ars Conjectandi). Earlier, Blaise Pascal had considered the special case where p = 1/2.

Definition of the Binomial Distribution

The binomial pdf is

where

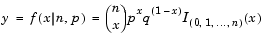
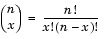and .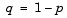

The binomial distribution is discrete. For zero and for positive integers less than n, the pdf is nonzero.

Parameter Estimation for the Binomial Distribution

Suppose you are collecting data from a widget manufacturing process, and you record the number of widgets within specification in each batch of 100. You might be interested in the probability that an individual widget is within specification. Parameter estimation is the process of determining the parameter, p, of the binomial distribution that fits this data best in some sense.

One popular criterion of goodness is to maximize the likelihood function. The likelihood has the same form as the binomial pdf above. But for the pdf, the parameters (n and p) are known constants and the variable is x. The likelihood function reverses the roles of the variables. Here, the sample values (the x's) are already observed. So they are the fixed constants. The variables are the unknown parameters. MLE involves calculating the value of p that give the highest likelihood given the particular set of data.

The function binofit returns the MLEs and confidence intervals for the parameters of the binomial distribution. Here is an example using random numbers from the binomial distribution with n = 100 and p = 0.9.

• r = binornd(100,0.9)
  
  r =
      88
  
  [phat, pci] = binofit(r,100)
  
  phat =
      0.8800
  
  pci =
      0.7998
      0.9364
  

The MLE for parameter p is 0.8800, compared to the true value of 0.9. The 95% confidence interval for p goes from 0.7998 to 0.9364, which includes the true value. Of course, in this made-up example we know the "true value" of p. In experimentation we do not.

Example and Plot of the Binomial Distribution

The following commands generate a plot of the binomial pdf for n = 10 and p = 1/2.

• x = 0:10;
  y = binopdf(x,10,0.5);
  plot(x,y,'+')
  
  
  

Beta Distribution

Chi-Square Distribution