Statistics Toolbox

linkage

Create hierarchical cluster tree

Syntax

• Z = linkage(Y)  
  Z = linkage(Y,'method') 
  

Description

Z = linkage(Y) creates a hierarchical cluster tree, using the Single Linkage algorithm. The input matrix, Y, is a distance vector of length 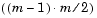-by-1, where m is the number of objects in the original dataset. You can generate such a vector with the pdist function. Y can also be a more general dissimilarity matrix conforming to the output format of pdist.

Z = linkage(Y,'method') computes a hierarchical cluster tree using the algorithm specified by 'method', where 'method' can be any of the following character strings that identify ways to create the cluster hierarchy. Their definitions are explained in Mathematical Definitions.

'single'	Shortest distance (default)
'complete'	Largest distance
'average'	Average distance
'centroid'	Centroid distance. The output Z is meaningful only if Y contains Euclidean distances.
'ward'	Incremental sum of squares

The output, Z, is an (m-1)-by-3 matrix containing cluster tree information. The leaf nodes in the cluster hierarchy are the objects in the original dataset, numbered from 1 to m. They are the singleton clusters from which all higher clusters are built. Each newly formed cluster, corresponding to row i in Z, is assigned the index m+i, where m is the total number of initial leaves.

Columns 1 and 2, Z(i,1:2), contain the indices of the objects that were linked in pairs to form a new cluster. This new cluster is assigned the index value m+i. There are m-1 higher clusters that correspond to the interior nodes of the hierarchical cluster tree.

Column 3, Z(i,3), contains the corresponding linkage distances between the objects paired in the clusters at each row i.

For example, consider a case with 30 initial nodes. If the tenth cluster formed by the linkage function combines object 5 and object 7 and their distance is 1.5, then row 10 of Z will contain the values (5, 7, 1.5). This newly formed cluster will have the index 10+30=40. If cluster 40 shows up in a later row, that means this newly formed cluster is being combined again into some bigger cluster.

Mathematical Definitions

The 'method' argument is a character string that specifies the algorithm used to generate the hierarchical cluster tree information. These linkage algorithms are based on various measurements of proximity between two groups of objects. If n_r is the number of objects in cluster r and n_s is the number of objects in cluster s, and x_ri is the ith object in cluster r, the definitions of these various measurements are as follows:

• Single linkage, also called nearest neighbor, uses the smallest distance between objects in the two groups.

• Complete linkage, also called furthest neighbor, uses the largest distance between objects in the two groups.

• Average linkage uses the average distance between all pairs of objects in cluster r and cluster s.

• Centroid linkage uses the distance between the centroids of the two groups.

• where

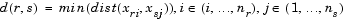
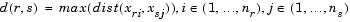
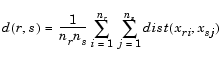
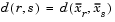
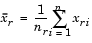
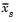• and is defined similarly.

  The centroid method can produce a cluster tree that is not monotonic. This occurs when the distance from the union of two clusters, 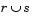, to a third cluster is less than the distance from either r or s to that third cluster. In this case, sections of the dendrogram change direction. This is an indication that you should use another method.

• Ward linkage uses the incremental sum of squares; that is, the increase in the total within-group sum of squares as a result of joining groups r and s. It is given by

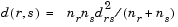
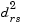• where is the distance between cluster r and cluster s defined in the Centroid linkage. The within-group sum of squares of a cluster is defined as the sum of the squares of the distance between all objects in the cluster and the centroid of the cluster.

Example

• X = [3 1.7; 1 1; 2 3; 2 2.5; 1.2 1; 1.1 1.5; 3 1];
  Y = pdist(X);
  Z = linkage(Y)
  Z =
      2.0000   5.0000   0.2000
      3.0000   4.0000   0.5000
      8.0000   6.0000   0.5099
      1.0000   7.0000   0.7000
     11.0000   9.0000   1.2806
     12.0000  10.0000   1.3454
  

See Also

cluster, clusterdata, cophenet, dendrogram, inconsistent, kmeans, pdist, silhouette, squareform

lillietest

logncdf