Statistics Toolbox

Hypothesis Test Assumptions

The difference between hypothesis test procedures often arises from differences in the assumptions that the researcher is willing to make about the data sample. For example, the Z-test assumes that the data represents independent samples from the same normal distribution and that you know the standard deviation, 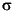. The t-test has the same assumptions except that you estimate the standard deviation using the data instead of specifying it as a known quantity.

Both tests have an associated signal-to-noise ratio

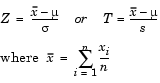
The signal is the difference between the average and the hypothesized mean. The noise is the standard deviation posited or estimated.

If the null hypothesis is true, then Z has a standard normal distribution, N(0,1). T has a Student's t distribution with the degrees of freedom, 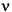, equal to one less than the number of data values.

Given the observed result for Z or T, and knowing the distribution of Z and T assuming the null hypothesis is true, it is possible to compute the probability (p-value) of observing this result. A very small p-value casts doubt on the truth of the null hypothesis. For example, suppose that the p-value was 0.001, meaning that the probability of observing the given Z or T was one in a thousand. That should make you skeptical enough about the null hypothesis that you reject it rather than believe that your result was just a lucky 999 to 1 shot.

There are also nonparametric tests that do not even require the assumption that the data come from a normal distribution. In addition, there are functions for testing whether the normal assumption is reasonable.

Hypothesis Test Terminology

Example: Hypothesis Testing