Optimization Toolbox

Nonlinear Inequality Constrained Example

If inequality constraints are added to Eq. 2-1, the resulting problem can be solved by the fmincon function. For example, find x that solves

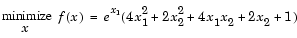
(2-2)

subject to the constraints

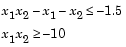
Because neither of the constraints is linear, you cannot pass the constraints to fmincon at the command line. Instead you can create a second M-file, confun.m, that returns the value at both constraints at the current x in a vector c. The constrained optimizer, fmincon, is then invoked. Because fmincon expects the constraints to be written in the form 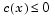, you must rewrite your constraints in the form

(2-3)

Step 1: Write an M-file confun.m for the constraints.

• function [c, ceq] = confun(x)
  % Nonlinear inequality constraints
  c = [1.5 + x(1)*x(2) - x(1) - x(2);     
       -x(1)*x(2) - 10];
  % Nonlinear equality constraints
  ceq = [];
  

Step 2: Invoke constrained optimization routine.

• x0 = [-1,1];     % Make a starting guess at the solution
  options = optimset('LargeScale','off');
  [x, fval] = ... 
  fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options) 
  

After 38 function calls, the solution x produced with function value fval is

• x = 
     -9.5474  1.0474 
  fval =
      0.0236
  

We can evaluate the constraints at the solution

• [c,ceq] = confun(x)
  c=
      1.0e-14 *
      0.1110
     -0.1776
  
  ceq =
       []
  

Note that both constraint values are less than or equal to zero; that is, x satisfies .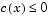

Unconstrained Minimization Example

Constrained Example with Bounds