

| Optimization Toolbox |   |
Nonlinear Equations with Jacobian
Consider the problem of finding a solution to a system of nonlinear equations whose Jacobian is sparse. The dimension of the problem in this example is 1000. The goal is to find x such that F(x) = 0. Assuming n = 1000, the nonlinear equations are
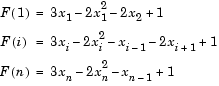
To solve a large nonlinear system of equations, F(x) = 0, use the large-scale method available in fsolve.
Step 1: Write an M-file nlsf1.m that computes the objective function values and the Jacobian.
function [F,J] = nlsf1(x); % Evaluate the vector function n = length(x); F = zeros(n,1); i = 2:(n-1); F(i) = (3-2*x(i)).*x(i)-x(i-1)-2*x(i+1)1+ 1; F(n) = (3-2*x(n)).*x(n)-x(n-1) + 1; F(1) = (3-2*x(1)).*x(1)-2*x(2) + 1; % Evaluate the Jacobian if nargout > 1 if nargout > 1 d = -4*x + 3*ones(n,1); D = sparse(1:n,1:n,d,n,n); c = -2*ones(n-1,1); C = sparse(1:n-1,2:n,c,n,n); e = -ones(n-1,1); E = sparse(2:n,1:n-1,e,n,n); J = C + D + E; end
Step 2: Call the solve routine for the system of equations.
xstart = -ones(1000,1); fun = @nlsf1; options = optimset('Display','iter','LargeScale','on','Jacobian','on'); [x,fval,exitflag,output] = fsolve(fun,xstart,options);
A starting point is given as well as the function name. The default method for fsolve is medium-scale, so it is necessary to specify 'LargeScale' as 'on' in the options argument. Setting the Display option to 'iter' causes fsolve to display the output at each iteration. Setting the Jacobian parameter 'on', causes fsolve to use the Jacobian information available in nlsf1.m.
The commands display this output:
Norm of First-order CG- Iteration Func-count f(x) step optimality Iterations 1 2 1011 1 19 0 2 3 16.1942 7.91898 2.35 3 3 4 0.0228027 1.33142 0.291 3 4 5 0.000103359 0.0433329 0.0201 4 5 6 7.3792e-007 0.0022606 0.000946 4 6 7 4.02299e-010 0.000268381 4.12e-005 5 Optimization terminated successfully: Relative function value changing by less than OPTIONS.TolFun
A linear system is (approximately) solved in each major iteration using the preconditioned conjugate gradient method. The default value for PrecondBandWidth is 0 in options, so a diagonal preconditioner is used. (PrecondBandWidth specifies the bandwidth of the preconditioning matrix. A bandwidth of 0 means there is only one diagonal in the matrix.)
From the first-order optimality values, fast linear convergence occurs. The number of conjugate gradient (CG) iterations required per major iteration is low, at most five for a problem of 1000 dimensions, implying that the linear systems are not very difficult to solve in this case (though more work is required as convergence progresses).
It is possible to override the default choice of preconditioner (diagonal) by choosing a banded preconditioner through the use of the parameter PrecondBandWidth. If you want to use a tridiagonal preconditioner, i.e., a preconditioning matrix with three diagonals (or bandwidth of one), set PrecondBandWidth to the value 1:
options = optimset('Display','iter','Jacobian','on',... 'LargeScale','on','PrecondBandWidth',1); [x,fval,exitflag,output] = fsolve(fun,xstart,options);
Norm of First-order CG- Iteration Func-count f(x) step optimality Iterations 1 2 1011 1 19 0 2 3 16.0839 7.92496 1.92 1 3 4 0.0458181 1.3279 0.579 1 4 5 0.000101184 0.0631898 0.0203 2 5 6 3.16615e-007 0.00273698 0.00079 2 6 7 9.72481e-010 0.00018111 5.82e-005 2 Optimization terminated successfully: Relative function value changing by less than OPTIONS.TolFun
Note that although the same number of iterations takes place, the number of PCG iterations has dropped, so less work is being done per iteration. See Preconditioned Conjugate Gradients.
 | Problems Covered by Large-Scale Methods | Nonlinear Equations with Jacobian Sparsity Pattern |  |